Geometric interpretations of linear regression and ANOVA

In this post, I explore the connection of linear regression to geometry.  In particular, I discuss the geometric meaning of fitted values, residuals, and degrees of freedom.  Using geometry, I derive coefficient interpretations and discuss omitted variable bias.  I finish by connecting ANOVA (both hypothesis testing and power analysis) to the underlying geometry.

Fitted values are projections

The fundamental geometric insight is that the predicted values \(\hat{Y}\) in a linear regression are the projection of the response \(Y\) onto the linear span of the covariates \(X_0, X_1, \ldots, X_n\).  I’ll call this the covariate space.  The residuals \(Y - \hat{Y}\) are therefore the projection of \(Y\) onto the orthogonal complement of the covariate space.  I’ll call this the residual space. The residual space contains the part of the data that is unexplained by the model.  To summarize, we can break \(Y\) into two orthogonal pieces: a component in the covariate space (the fitted values from the regression of \(Y \sim X_0 + \ldots + X_n\)) and a component in the residual space (the residuals of the regression \(Y \sim X_0 + \ldots + X_n\)).

The fitted values are an orthogonal projection onto the covariate space because the two-norm between \(Y\) and \(\hat{Y}\) is minimized in the fitting process (the two-norm distance from a point to a surface is minimized when the point is orthogonal to the surface).  I’ll also note that the linear regression equations are the same as the projection equations from linear algebra.  In regression, the parameter \(\hat{\beta}\) satisfies \(X^T X \hat{\beta} = X^T Y\) and so \(\hat{Y} = X \hat{\beta} = X (X^T X)^{-1} X^T Y\).  From linear algebra, \(P = X (X^T X)^{-1} X^T\) is the matrix that projects onto the column space of \(X\).  The connection to orthogonal projections is because of the two-norm: robust regression using a Huber penalty or lasso regression using a one-norm penalty do not have the same geometric interpretation.

The geometry of nested models

Consider a nested model: a small model and a big model, with the covariate space \(L_{\text{small}}\) of the small model contained in the covariate space \(L_{\text{big}}\) of the big model.  For example, the small model might be the regression \(Y \sim X_0 + X_1\) and the big model might be the regression \(Y \sim X_0 + X_1 + X_2\).  Define the delta covariate space \(L_{\text{delta}}\) to be the orthogonal complement of \(L_{\text{small}}\) in \(L_{\text{big}}\).  The picture below shows the small model covariate space, the delta covariate space (orthogonal to the small model covariate space), the big model covariate space (composed of the small model covariate space and the delta covariate space), and the residual space (orthogonal to everything).

From properties of orthogonal projections, it is clear the fitted values (aka projections of \(Y\)) in the small and big model are related by \(\hat{Y}_{\text{big}} = \hat{Y}_{\text{small}} + \hat{Y}_{\text{delta}}\).  This simple geometric equation 1) implies that one-dimensional linear regression is sufficient when covariates are orthogonal, 2) shows that the coefficient on (for example) \(X_n\) in the multivariate linear regression \(Y \sim X_0 + \ldots X_n\) is the effect of \(X_n\) on \(Y\) after controlling for the other covariates, and 3) quantifies omitted variable bias.

Coefficient interpretation and omitted variable bias

Consider the small model \(Y \sim X_0 + \ldots X_{n-1}\) and the large model \(Y \sim X_0 + X_2 + \ldots X_n\), which has one additional covariate \(X_n\).  From the geometric relation \(\hat{Y}_{\text{big}} = \hat{Y}_{\text{small}} + \hat{Y}_{\text{delta}}\), we’ll derive coefficient interpretation and omitted variable bias.  Write the fitted values from the small model as \(\hat{Y}_{\text{small}} = s_0 X_0 + \ldots s_{n-1} X_{n-1}\), where the coefficients \(s_i\) are from the regression \(Y \sim  X_0 + \ldots X_{n-1}\).  We consider two cases: one where the added covariate is orthogonal to the previous covariates and one where it is not.

Added covariate \(X_n\) is orthogonal to previous covariates 

If the added covariate \(X_n\) is orthogonal to the previous covariates \(X_0, \ldots, X_{n-1}\), then the delta covariate space is the line spanned by \(X_n\) (i.e., the delta covariate space space is simply the space spanned by the additional covariate).  In this case, \(\hat{Y}_{\text{delta}} = b_n X_n\), where \(b_n\) is the coefficient from the regression \(Y \sim X_n\).  (\(b_n = \frac{Y \cdot X_n}{ X_n \cdot X_n}\).)  Thus \(\hat{Y}_{\text{big}} = \hat{Y}_{\text{small}} + \hat{Y}_{\text{delta}} =s_0 X_0 + \ldots s_{n-1} X_{n-1} + b_n X_n\).  The coefficients for the big regression \(Y \sim X_0 + \ldots + X_n\) are \(b_0 = s_0, b_1 = s_1, \ldots, b_{n-1}=s_{n-1}\) and \(b_n\).  In this case, the coefficients in the big model are uncoupled in that the coefficients corresponding to small model covariates can be computed separately from the coefficient on the new covariate \(X_n\).

In general, orthogonal groups of coefficients are uncoupled and can be handled separately in regression.  In the special case where all covariates are pairwise orthogonal, the coefficients in the big model can be computed by running \(n\) simple linear regressions \(Y \sim X_i\).

Finally, I want to discuss what happens when the regression includes an intercept term.  In this case, “orthogonal” is replaced by “uncorrelated.”  Groups of uncorrelated variables can be handled separately, and if all covariates in a multivariate linear regression are pairwise uncorrelated, each coefficient can be computed as the slope in a simple linear regression \(Y \sim 1 + X_i\).  To see why, consider the projection of \(Y\) onto the covariate space spanned by \(1, X_1, \ldots, X_n\), where the covariates \(X_1, \ldots, X_n\) are pairwise uncorrelated.  The covariate space doesn’t change when we center each covariate by subtracting off its mean (i.e., its projection onto 1).  Uncorrelated means the centered covariates are pairwise orthogonal, and each centered covariate is orthogonal to 1 as well.  The coefficient on the centered covariate \(X_i - \bar{X_i}\) comes from the projection of \(Y\) onto \(X_i - \bar{X_i}\).  Equivalently, it is the slope on \(X_i\) in the regression \(Y \sim 1 + X_i\) (think about why this is geometrically).  To summarize, the regression \(Y \sim 1 + X_1 + \ldots + X_n\) where the covariates \(X_i\) are pairwise uncorrelated can be computed by running \(n\) simple linear regressions \(Y \sim 1 + X_i\).  This slope is \(\frac{Y \cdot (X_i - \bar{X_i})}{(X_i - \bar{X_i}) \cdot(X_i - \bar{X_i})} =\frac{(Y - \bar{Y}) \cdot (X_i - \bar{X_i})}{(X_i - \bar{X_i}) \cdot(X_i - \bar{X_i})} = \frac{\text{Cov}(Y,X_i)}{\text{Var}(X_i)}\).

Added covariate \(X_n\) is not orthogonal to previous covariates 

Now consider the case where \(X_n\) is not orthogonal to the previous covariates.  The delta covariate space is spanned by \(X_n\) minus the projection of \(X_n\) onto the covariate space of the previous covariates.  In other words, the delta covariate space is spanned by the residuals \(\tilde X_n\) in the regression \(X_n \sim X_0 + \ldots X_{n-1}\) (write \(\tilde{X_n} = X_n - a_0 X_0 - \ldots a_{n-1} X_{n-1}\)).  The projection onto the delta covariate space \(\hat Y_{\text{delta}} = b_n \tilde X_n\) where \(b_n\) is the coefficient in the regression \(Y \sim \tilde X_n\).  Thus

\[\begin{aligned} \hat{Y}_{\text{big}} &= \hat{Y}_{\text{small}} + \hat{Y}_{\text{delta}} \\ &= (s_0 X_0 + \ldots + s_{n-1} X_{n-1}) + b_n \tilde X_n\\ &= (s_0 -  b_n a_0) X_0 + \ldots + (s_{n-1} - b_n a_{n-1}) X_{n-1} + b_n X_n \\ &:= b_0 X_0 + \ldots b_n X_n \end{aligned}\]

This explains both 2) and 3) above.  The coefficient \(b_n\) on a covariate in a regression model can be obtained by regressing \(Y\) on the residuals \(\tilde X_n\) from the regression of \(X_n\) on the other covariates.  This is often summarized by saying \(b_n\) is the effect of \(X_n\) on \(Y\) after controlling for the other covariates.  Rather than regress \(Y \sim \tilde{X_n}\), we could instead regress \(Y \sim X_0 + \tilde{X_n}\) and grab the coefficient on \(\tilde{X_n}\).  This works because \(\tilde{X_n}\) is orthogonal to \(X_0\).  In models that include an intercept \(X_0 = 1\), this is what is often done (but is unnecessary).

Often the residuals \(\tilde Y\) (from the regression \(Y \sim X_0 + \ldots + X_{n-1}\)) are regressed on the residuals \(\tilde X_{n}\) to find \(b_n\) (see my earlier post on Interpreting regression coefficients), rather than just regressing \(Y\) on \(\tilde X_{n}\).  These two regressions estimate the same slope.  (Geometrically this is easy to see: in one case, we are projecting \(Y\) onto the delta covariate space spanned by \(\tilde X_{n}\) and in the other, we are projecting \(\tilde Y\).  Both projections are the same because \(Y\) and \(\tilde Y\) differ by a vector in the small covariate space, which is orthogonal to the delta covariate space we’re projecting onto.)

We also see how including a new covariate updates the coefficients in the model: \(b_{n-1} = s_{n-1} - b_n a_{n-1}\).  The estimated effect \(s_{n-1}\) in the small model does not control for the omitted variable \(X_n\) and must be reduced by \(b_n a_{n-1}\) in the big model.  The omitted variable bias \(b_n a_{n-1}\) is the effect of the included variable \(X_{n-1}\) on the response \(Y\) acting through the omitted variable \(X_n\) (effect of included on omitted (\(a_{n-1}\)) times the effect of omitted on response (\(b_n\))).

ANOVA

ANOVA was first developed as a way to partition variance in experimental design and later extended to a method to compare linear models (classical ANOVA in experiment design is a special case of the “model comparison” ANOVA where treatments are encoded with dummy factors in a regression model).  Suppose we have two nested models: a small model (with degrees of freedom \(\text{df}_{\text{small}}\)) contained in a larger one (with degrees of freedom \(\text{df}_{\text{big}}\)).  (The degrees of freedom in a linear model is the dimension of its covariate space or equivalently the number of independent covariates.  If the model includes an intercept (which is not considered a covariate in statistics), the degrees of freedom is the number of independent covariates plus 1 (because the intercept is a covariate from a geometric perspective)).  The larger model will have smaller residuals, but the question is if they are so much smaller that we reject the small model.

Model comparison

The “regression sum of squares” is the difference in sum squared residuals between the small and large models:

\[\begin{aligned} \text{SS}_{\text{regression}} &= \text{SS}_{\text{small}} - \text{SS}_{\text{big}} \\&=  \| Y - \hat{Y}_{\text{small}} \|^2 -  \| Y - \hat Y_{\text{big}} \|^2.  \end{aligned}\]

The F-statistic (named after statistician R. A. Fisher) compares regression sum of squares (additional variation explained by the larger model) to the residuals in the larger model (unexplained variation by the larger model):

\[\begin{aligned} F &= \frac{\text{SS}_{\text{regression}} / (\text{df}_{\text{big}} - \text{df}_{\text{small}}) }{\text{SS}_{\text{big}} / (n-\text{df}_{\text{big}}) } \\ &=  \frac{(\text{SS}_{\text{small}} - \text{SS}_{\text{big}}) /(\text{df}_{\text{big}} - \text{df}_{\text{small}}) }{\text{SS}_{\text{big}} / (n-\text{df}_{\text{big}}) }. \end{aligned}\]

The regression sum of squares is the square length of the projection of \(Y\) onto the delta covariate space.  Recall the geometric equation \(\hat{Y}_{\text{big}} = \hat{Y}_{\text{small}} + \hat{Y}_{\text{delta}}\).  In terms of residuals: the residuals in the small model can be decomposed into the residuals in the big model plus the fitted values in the delta model.  Thus \(\text{SS}_{\text{small}} = \| Y - \hat{Y}_{\text{small}} \|^2 = \| (Y - \hat{Y}_{\text{big}}) + \hat{Y}_{\text{delta}} \|^2\).  The residuals in the big model are orthogonal to \(\hat{Y}_{\text{delta}}\), which is contained in the big model.  By the Pythagorean Theorem, we have \(\text{SS}_{\text{small}} = \text{SS}_{\text{big}} + \| \hat{Y}_{\text{delta}} \|^2\) and so \(\text{SS}_{\text{regression}} = \| \hat{Y}_{\text{delta}} \|^2\).  In words, the sum of squares of regression is the square length of the projection of \(Y\) onto the delta covariate space between the small and big models.  The \(F\) statistic is therefore also equal to

\[F = \frac{\| \hat{Y}_{\text{delta}} \|^2 / (\text{df}_{\text{big}} - \text{df}_{\text{small}}) }{\text{SS}_{\text{big}} /(n-\text{df}_{\text{big}}) }.\]

Intuitively, if the F-statistic is near 1, then the big model is not much of an improvement over the small model because the difference in errors between the two models is on the order of the error in the data.  To analyze the F-statistic, we need to assume a statistical model that generates the data.  In the regression framework, we assume \(Y \sim N(\mu, \sigma^2 I)\), where \(\mu\) lies in some linear subspace.  The small model is correct if \(\mu\) belongs to the covariate space of the small model.  The approach is as follows: under the assumption that the small model is correct (null model), we compute the distribution of the F-statistic (spoiler: it follows an F-distribution).  This is called the null distribution of the F-statistic.  We then compare the observed F-statistic to the null distribution and reject the small model if the observed F-statistic is “extreme.”

Projections (and indeed any linear transformation) of normal random variables are normal. The regression sum of squares is the square length of the normal random variable \(\hat Y_{\text{delta}} = \text{proj}_{L_{\text{delta}}}(Y)\).  Let \(P\) be the projection matrix so that \(\hat Y_{\text{delta}} = P Y\).  If the small model is correct, \(Y \sim N(\mu, \sigma^2 I)\) with \(\mu \in L_{\text{small}}\).  Then \(P \hat Y_{\text{delta}} \sim N(P \mu, \sigma^2 P P^T) = N(P \mu, \sigma^2 P)\) (projection matrices satisfy \(P = P^T\) and \(P^2 = P\)).  By the spectral theorem from linear algebra, we can write \(P = Q \Lambda Q^T\) with \(Q\) orthogonal and \(\Lambda = \text{Diag}(1,1,\ldots, 1, 0, \ldots, 0)\), a diagonal matrix with \(\text{df}_{\text{big}} - \text{df}_{\text{small}}\) 1s followed by 0s on the main diagonal.  Geometrically, we are expressing the projection in three steps: first rotate so the space onto which we are projecting is the standard subspace \(\mathbb{R}^{\text{df}_{\text{big}} - \text{df}_{\text{small}}}\), do the simple projection onto \(\mathbb{R}^{\text{df}_{\text{big}} - \text{df}_{\text{small}}}\) by taking the first \(\text{df}_{\text{big}} - \text{df}_{\text{small}}\) coordinates and setting the rest to 0, and then rotate back.

The rotated vector \(Q^T \hat{Y}_{\text{delta}}\) is distributed \(N(Q^T P \mu, \sigma^2 \Lambda)\).  Under the assumption that the small model holds and \(\mu \in L_{\text{small}}\), the projection of \(\mu\) onto \(L_{\text{delta}}\) is 0 and so \(Q^T \hat{Y}_{\text{delta}} / \sigma \sim N(0, \Lambda)\).  The square length \(\| \hat{Y}_{\text{delta}} \|^2 / \sigma^2\) is distributed \(\chi^2_{\text{df}_{\text{big}} - \text{df}_{\text{small}}}\) (a \(\chi^2_d\) random variable with \(d\) degrees of freedom is the sum of squares of \(d\) independent standard normal random variables).

The denominator in the F-statistic is \(\text{SS}_{\text{big}}\), the square length of the residuals in the big model.  The residuals in the big model is the projection of \(Y\) onto the orthogonal complement of \(L_{\text{big}}\) (which I called the residual space before).  Both the small model covariate space and delta covariate space are contained in the big model covariate space.  The residual space is therefore orthogonal to all these spaces.  The variance normalized residuals \(\text{SS}_{\text{big}} / \sigma^2\) for the big model follow a \(\chi^2_{n - \text{df}_{\text{big}}}\) distribution.

The F-statistic is a ratio of a \(\chi^2_{ \text{df}_{\text{big}} -\text{df}_{\text{small}} } / (\text{df}_{\text{big}} -\text{df}_{\text{small}})\) random variable to a \(\chi^2_{n - \text{df}_{\text{big}}} / (n - \text{df}_{\text{big}})\) random variable.  This is the definition of an \(F_{\text{df}_{\text{big}} - \text{df}_{\text{small}},\ n - \text{df}_{\text{big}}}\) distribution.  (A careful reader will notice that to be F distributed, the numerator and denominator \(\chi^2\) distributions must be independent.  This is the case because the two come from independent normal random variables: the numerator from the projection onto the delta covariate space and the denominator from the projection onto the residual space.  These two spaces are orthogonal, and orthogonal zero-mean vectors are uncorrelated.  In the case of normal random variables, uncorrelated means independent.)

ANOVA is often organized in an ANOVA table.  In practice, you consider a sequence of nested linear models \(M_0 \subset M_1 \subset M_2 \subset M_3 \subset \ldots \subset M_k\).  The inner-most model \(M_0\) is always the intercept model, in which \(Y\) is estimated with its mean \(\bar{Y}\).  The table has one row for each model \(M_i\) (excluding \(M_0\)) and a final row for the residuals.  The row for \(M_i\) contains information about the numerator of the F-statistic where the big model is \(M_i\) and the small model is the previous model \(M_{i-1}\).  It contains the regression sum of squares \(\text{SS}_{\text{regression}} = \text{SS}_{M_{i}} - \text{SS}_{M_{i-1}}\), the degrees of freedom \(\text{df}_{\text{regression}} = \text{df}_{M_i} - \text{df}_{M_{i-1}}\), the mean square error \(\text{SS}_{\text{regression}} / \text{df}_{\text{regression}}\), the F-statistic, and a P-value.  Unlike we discussed in the previous paragraphs, the F-statistic in the \(i\)th row of an ANOVA table does not divide the mean square error for regression by the mean square error for the residuals in the big model \(M_i\).  The denominator instead uses the residuals from the biggest model in the table \(M_k\), which are stored in the last row of the table.  The last row contains the residual sum of squares \(\text{SS}_{M_k}\), the residual degrees of freedom \(n - \text{df}_{M_k}\), and the residual mean square error \(\text{SS}_{M_k} / (n - \text{df}_{M_k})\), an estimate of \(\sigma^2\).  Here is an example.

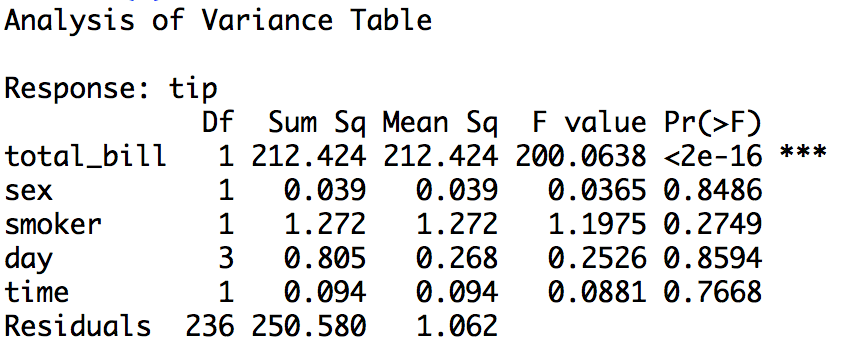
The ANOVA table above is a sequential ANOVA table, in which the models are nested by successively adding new covariates.  The intercept model \(M_0\) (not a row in the table) is \(\text{tip} \sim 1\), the first model \(M_1\) is \(\text{tip} \sim 1 + \text{total_bill}\), the second model is \(M_2\) is \(\text{tip} \sim 1 + \text{total_bill} + \text{sex}\), and so forth.

Power analysis

We just discussed the distribution of the F-statistic under the small model.  We can reject the small model if the observed F-statistic is extreme for what we expect the F-statistic to look like under the small model.  If we don’t reject the small model, it doesn’t mean that the small model is correct; it just means that we have insufficient evidence to reject it.  The power of a test is the probability that the test rejects the small model (null model) when the big model is true (the alternative model is true).  The probability that we reject the small model if the big model is true will depend on how far the true mean is from the small model covariate space.  Rejection is harder if the true mean is near, but not in, the small model covariate space.

To do power analysis, we assume that the mean \(\mu \in L_{\text{big}} \setminus L_{\text{small}}\) and work out the distribution of the F-statistic.  The denominator of the F-statistic (square norm of the projection of \(Y\) onto the residual space) is still a \(\chi^2\) distribution because \(\mu\) is orthogonal to the residual space.  The numerator of the F-statistic is the square norm of \(Q^T \hat{Y}_{\text{delta}}\), which is distributed \(N(Q^T P \mu, \sigma^2 \Lambda)\).  Under the big model, \(Q^T P \mu\) is no longer 0 and we don’t get a \(\chi^2\) distribution.  Instead we get a noncentral \(\chi^2_{\text{df}_{\text{big}} - \text{df}_{\text{small}}}( \| P \mu \|^2)\) distribution with \(\text{df}_{\text{big}} - \text{df}_{\text{small}}\) degrees of freedom and noncentrality parameter \(\| P \mu \|^2\).  Notice that \(\| P \mu \|^2\) is just the square distance of \(\mu\) to the small model covariate space.  The F-statistic follows a noncentral F distribution.

Written on August 5th, 2018 by Scott Roy