Maximum likelihood estimation with censored data

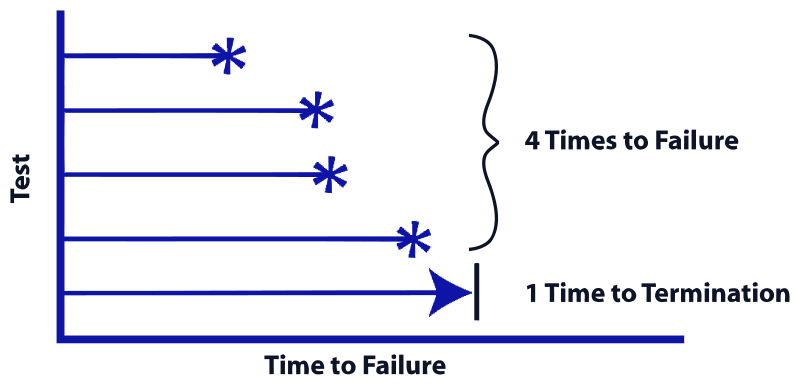
Suppose I’m tasked with analyzing failure times for hard drives in a datacenter.  I track 100 hard drives over a 2 year period, and if a hard drive fails, I record when. If the hard drive has not failed by the 2 year mark, I don’t when when it will fail, just that its failure time is more than 2 years. We say the failure times for the hard drives remaining at the 2 year mark are censored.

I decide to fit an exponential model to the failure times, and I fit the parameter with maximum likelihood estimation. The exponential distribution with rate parameter \(\beta\) has density \(f(x \vert \beta) = \beta e^{-\beta x}\). To keep things simple, suppose I observe failures for the first 75 hard drives (with failure times \(x_1,\ldots, x_{75}\) in years),  and the last 25 hard drives have censored failure times.  The likelihood is

\[\begin{aligned} f(x\vert \beta) &= \left( \prod_{i=1}^{75} f(x_i \vert \beta) \right) \textbf{P}(X \geq 2 \vert \beta)^{25} \\ &= \left(\prod_{i=1}^{75} \beta e^{-\beta x_i} \right) \left( e^{-2 \beta} \right)^{25}. \end{aligned}\]

The negative log likelihood is

\[l(x\vert \beta) = \left(\sum_{i=1}^{75} x_i + 25 \times 2 \right) \beta - 75 \log (\beta),\]

which means the MLE is

\[\hat{\beta} = \frac{75}{\sum_{i=1}^{75} x_i + 25 \times 2}.\]

I want to compare this to the estimates I get if I improperly handle the censored data in each of the following ways:

• Discard the censored observations.
• Record the censored observations as 2 years.

If I discard the censored observations, the negative log likelihood and MLE are:

\[\begin{aligned} l(x \vert \beta) &= \left(\sum_{i=1}^{75} x_i \right) \beta - 75 \log (\beta) \\ \hat{\beta} &= \frac{75}{\sum_{i=1}^{75} x_i}. \end{aligned}\]

In this case, I over-estimate the exponential rate \(\beta\) (i.e., under-estimate the mean \(\frac{1}{\beta}\)).  I also under-estimate the mean if I replace the censored observations with 2 years:

\[\begin{aligned} l(x \vert \beta) &= \left(\sum_{i=1}^{75} x_i + 25 \times 2 \right) \beta - 100 \log (\beta) \\ \hat{\beta} &= \frac{100}{\sum_{i=1}^{75} x_i+ 25 \times 2}. \end{aligned}\]

We can deal with other kinds of censoring in MLE calculations, too. Suppose we don’t know what \(x_i\) is, but we just know that it lies between 3 and 4. We would then use \(\textbf{P}( 3 \leq X \leq 4 \vert \beta)\) instead of \(f(x_i \vert \beta)\) in the likelihood product.

Written on April 20th, 2018 by Scott Roy