statsandstuff a blog on statistics and machine learning

The relationship between correlation, mutual information, and p-values

Feature selection is often necessary before building a machine learning or statistical model, especially when there are many, many irrelevant features. To be more concrete, suppose we want to predict/explain some response \(Y\) using some features \(X_1, \ldots, X_k\). A natural first step is to find the features that are “most related” to the response and build a model with those. There are many ways we could interpret “most related”:

In this post, I want to discuss why any of the above approaches should work well. The basic insight is that:

The post is organized into three scenarios:

Both variables are binary

In this section, we assume both the feature \(X \in \{0,1\}^N\) and response \(Y \in \{0, 1\}^N\) are binary. We focus on one feature to highlight the relation between the chi-squared test, the correlation, the G-test, and mutual information. We can summarize the relation between binary variables in a contingency table:

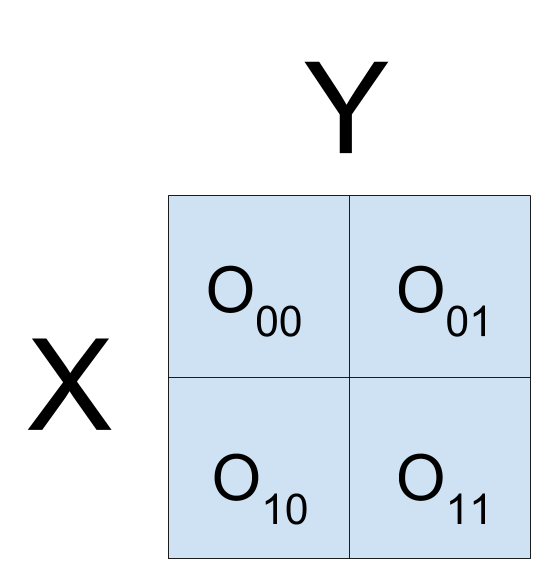
In the table \(O_{ij}\) denotes the number of observations where \(X = i\) and  \(Y = j\). In addition, we let \(\cdot\) denote summation over an index; so \(O_{i \cdot}\) is the sum of the \(i\)th row and \(O_{\cdot j}\) is the sum of the \(j\)th column. 

Correlation and the chi-squared test

In the context of binary variables, the Pearson correlation is often called the “phi coefficient” and can be computed from the contingency table itself:

\[\phi = \frac{O_{00} O_{11} - O_{01} O_{10}}{\sqrt{O_{0\cdot} O_{\cdot 0} O_{1 \cdot} O_{\cdot 1}}}.\]

The phi coefficient is a measure of association between \(X\) and \(Y\); it is a product of counts where \(X\) and \(Y\) agree minus a product of counts where they disagree, normalized by row and column sums so that the value is between -1 and 1.

Another common way to measure the association between two binary variables is the chi-squared test of independence, introduced by Karl Pearson in 1900. As a reminder, the chi-squared test statistic is

\[\chi^2 = \sum \frac{(O_{ij} - E_{ij})^2}{E_{ij}},\]

where

\[E_{ij} = N \left( \frac{O_{i \cdot}}{N} \right) \left( \frac{O_{\cdot j}}{N} \right) := N r_i c_j\]

is the expected number observations in cell \((i,j)\) under the assumption that \(X\) and \(Y\) are independent.

For fixed sample size \(N\), the phi coefficient is just a reparametrization of the the chi-squared statistic:

\[\phi = \sqrt{\frac{\chi^2}{n}}.\]

This is easy to show by expanding the chi-squared statistic.  (For those who want to work out the algebra, the following relation is useful:

\[O_{i \cdot} O_{\cdot j} = n O_{ij} + s_{ij} \Delta,\]

where \(s_{ij}\) is either 1 (if \(i \neq j\) ) or -1 (\(i = j\) ) and \(\Delta = O_{00} O_{11} - O_{01} O_{10}\) is the determinant of the contingency table.)

Tying this to the theme of the post, suppose we have a binary response \(Y\) and binary features \(X_1, \ldots, X_k\). Ranking the features by p-value from a chi-squared test with the response is equivalent to ranking the features by absolute correlation with the response. For fixed sample size \(N\), the p-value itself is a measure of association strength.

Difference in proportions test

When both \(X\) and \(Y\) are binary, we can view \(X\) as defining group membership and \(Y\) as defining an outcome. For example, suppose \(X\) indicates whether someone smokes and \(Y\) indicates if they have lung cancer. In this case, the association between \(X\) and \(Y\) is captured in the difference in the proportion \(p_1\) of smokers who get lung cancer and the proportion \(p_0\) of non-smokers who do. The difference in proportions test statistic

\[T = \frac{p_1 - p_0}{\sqrt{p(1-p) \left( \frac{1}{N_1} + \frac{1}{N_0} \right)}}\]

tests if \(p_1\) is different than \(p_0\) and is approximately distributed standard normal under the null hypothesis \(H_0 : p_0 = p_1\).

The statistic \(T\) is just the square root of the chi-squared test statistic \(\chi^2\) and so the two tests are equivalent. (An easy way to see this is to show that \(T = \sqrt{N} \phi\) by writing \(p_0\), \(p_1\), \(p\), \(N_0\), and \(N_1\) in terms of the cells \(O_{ij}\) of the contingency table.)

Mutual information and the G-test

The likelihood ratio test (LRT) is an alternative to the chi-squared test of independence. The resulting test statistic is the so-called G-statistic:

\[G = 2 \sum O_{ij} \log \left( \frac{O_{ij}}{E_{ij}} \right).\]

The relation

\[G = 2 N \ \text{MI}(X, Y)\]

between \(G\) and the mutual information between \(X\) and \(Y\) is immediate (\(\text{MI}(X, Y)\) is the Kullback-Leibler divergence of the product of the marginal distributions from the joint distribution). It follows that the ranking among features induced by mutual information with the response is the same as the ranking induced by p-values computed via a G-test.

In practice this is often similar to the rankings induced by correlation/proportion tests/chi-squared tests because the chi-squared test statistic is the second-order Taylor approximation of the G-statistic (expand the log term about 1).

One variable is binary

In this section, we assume the feature \(X \in \{0,1\}^N\) is a binary vector and the response \(Y \in \mathbb{R}^N\) is real-valued. (We could instead assume \(Y\) is binary and \(X\) is real-valued.) As with the difference in proportions test, we can view \(X\) as defining two groups (e.g., a treatment and control group in an experiment) and \(Y\) as defining some continuous outcome. A measure of association between \(X\) and \(Y\) is captured in the difference between the mean outcome \(\bar{Y}_1\) in treatment and the mean outcome in control \(\bar{Y}_0\). This difference is often assessed with a two-sample t-test using the test statistic

\[T = \frac{\bar{Y}_{1\cdot} - \bar{Y}_{0\cdot}}{\sqrt{S_p^2 \left(\frac{1}{N_1} + \frac{1}{N_0} \right)}}.\]

Here \(S^2_p\) denotes the pooled sampled variance

\[S^2_p = \frac{\sum_{i=0}^1 \sum_{j=1}^{N_j} (Y_{ij} - \bar{Y}_{i\cdot})^2}{N-2}.\]

As with the chi-squared/difference in proportions tests before, the t-statistic \(T\) is a reparametrization of the Pearson sample correlation \(r\):

\[r = \frac{T}{\sqrt{N-2 + T^2}}.\]

Before we walk through the derivation, we define some notation.  The vector \(X\) splits the observations \(Y\) into two groups: \(\{ Y_i : X_i = 0 \}\) and \(\{ Y_i : X_i = 1 \}\) .  Let \(N_0\) and \(N_1\) be the respective sizes of these groups.  We reindex the observations \(Y\) using notation from ANOVA.  We let \(Y_{ij}\) denote the \(j\) th observation (\(j = 1\ldots N_j\) ) from the \(i\) th group (\(i = 0, 1\) ).  The notation \(\bar{Y}_{i\cdot}\) denotes the mean of \(Y\) over the \(i\) th group and \(\bar{Y}_{\cdot \cdot}\) denotes the overall mean of \(Y\).

We can write

\[r = \frac{\bar{Y}_{1\cdot} - \bar{Y}_{0\cdot}}{\sqrt{(N-1) S^2 \left(\frac{1}{N_1} + \frac{1}{N_0} \right)}},\]

where \(S^2 = \frac{1}{n-1} \sum_{i=1}^N (Y_i - \bar{Y})^2\) is the sample variance.  This resembles the two sample t-statistic (which hints at the connection), but has the sample variance \(S^2\) instead of the pooled variance \(S^2_p\).

We relate \(S^2\) and \(S^2_p\) with the following sum of squares partition (derivation in the appendix):

\[(N-1) S^2 \left( \frac{1}{N_1} + \frac{1}{N_0} \right) = (N-2) S_p^2 \left( \frac{1}{N_1} + \frac{1}{N_0} \right) + (\bar{Y}_{1\cdot} - \bar{Y}_{0\cdot})^2.\]

Using this partition to rewrite the denominator in the correlation expression and dividing numerator and denominator by \(\sqrt{S_p^2 \left( \frac{1}{N_1} + \frac{1}{N_0} \right)}\) yields

\[\begin{aligned} r &= \frac{\bar{Y}_{1\cdot} - \bar{Y}_{0\cdot}}{\sqrt{(N-1) S^2 \left(\frac{1}{N_1} + \frac{1}{N_0} \right)}} \\ &= \frac{(\bar{Y}_{1\cdot} - \bar{Y}_{0\cdot}) / \sqrt{S_p^2 \left( \frac{1}{N_1} + \frac{1}{N_0} \right)}}{\sqrt{N-2 + (\bar{Y}_{1\cdot} - \bar{Y}_{0\cdot})^2 / \left(S_p^2 \left( \frac{1}{N_1} + \frac{1}{N_0} \right)\right)}} \\ &= \frac{T}{\sqrt{N-2 + T^2}}. \end{aligned}\]

Both variables are real-valued

Suppose we regress \(Y \sim 1 + X\) and get slope \(\hat{\beta}\). We can use a t-test to test if the slope is different than 0. The p-value we get is just a reparametrization of correlation.

To make matters simple, let \(SXX = \sum_{i=1}^N (X_i - \bar{X})^2\) be the sum of squares for \(X\) (and similarly for \(SYY\) ), \(SXY = \sum_{i=1}^N (X_i - \bar{X}) (Y_i - \bar{Y})\) , and \(RSS = \sum_{i=1}^N (Y_i - \hat{Y}_i)^2\) be the residual sum of squares.

We can write the slope \(\hat{\beta} = \frac{SXY}{SXX}\) and the correlation between \(X\) and \(Y\) as \(r = \hat{\beta} \sqrt{\frac{SXX}{SYY}}.\)

To test whether \(\hat{\beta}\) is nonzero, we see how many standard errors it is from 0.  The standard error of \(\hat{\beta}\) is \(\text{se}(\hat{\beta}) = \sqrt{\frac{RSS}{(N-2) SXX}}\) and the test statistic is

\[T = \frac{\hat{\beta}}{\text{se}(\hat{\beta})} = \hat{\beta} \sqrt{\frac{SXX}{RSS / (N-2)}}.\]

This reduces to the two-sample t-statistic when \(X\) is binary and follows a t-distribution with \(N-2\) degrees of freedom.

Dividing numerator and denominator in the expression for \(r\) by \(\sqrt{RSS / (N-2)}\) (after rewriting \(SYY = RSS + \hat{\beta}^2 SXX\) ) we get

\[\begin{aligned} r &= \hat{\beta} \sqrt{\frac{SXX}{SYY}} \\ &= \frac{\hat{\beta} \sqrt{\frac{SXX}{RSS / (N-2)}}}{\sqrt{N-2 + \hat{\beta}^2 \frac{SXX}{RSS / (N-2)} }} \\ &= \frac{T}{\sqrt{N-2 + T^2}}.  \end{aligned}\]

Summary

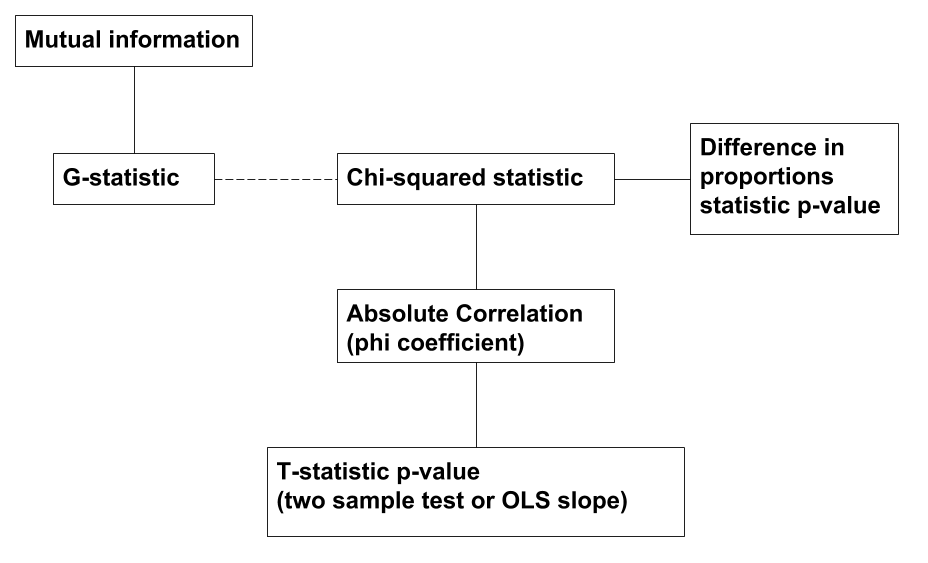
In this post, we discussed various ways of measuring association between a response \(Y\) and predictors \(X_1, \ldots, X_p\) in the context of feature selection. We showed that all the methods are more or less equivalent, which we summarize in the following diagram.

A solid connector indicates the two quantities are reparametrizations of each other (i.e., there is an increasing function that maps one to the other). The dashed line between the G-statistic and the chi-squared statistic indicates that these quantities are approximately equivalent and so give similar rankings in practice.

Appendix: partitioning the sum of squares

Partitioning the variation is fundamental in ANOVA and regression analysis and is a simple consequence of the Pythagorean theorem.  Define the following three vectors

\[Y = \begin{bmatrix} \begin{pmatrix} Y_{11} \\ Y_{12} \\ \vdots \\ Y_{1 N_1} \end{pmatrix} \\ \begin{pmatrix} Y_{21} \\ Y_{22} \\ \vdots \\ Y_{2 N_2} \end{pmatrix} \end{bmatrix} \quad Y_{\text{trt}} = \begin{bmatrix} \begin{pmatrix} \bar{Y}_{1 \cdot} \\ \bar{Y}_{1 \cdot} \\ \vdots \\ \bar{Y}_{1 \cdot} \end{pmatrix} \\ \begin{pmatrix} \bar{Y}_{2 \cdot} \\ \bar{Y}_{2 \cdot} \\ \vdots \\ \bar{Y}_{2 \cdot} \end{pmatrix} \end{bmatrix} \quad  \bar{Y}_{\cdot \cdot} = \begin{bmatrix} \begin{pmatrix} \bar{Y}_{\cdot \cdot} \\ \bar{Y}_{\cdot \cdot} \\ \vdots \\ \bar{Y}_{\cdot \cdot} \end{pmatrix} \\ \begin{pmatrix} \bar{Y}_{\cdot \cdot} \\ \bar{Y}_{\cdot \cdot} \\ \vdots \\ \bar{Y}_{\cdot \cdot} \end{pmatrix} \end{bmatrix}\]

The vectors \((Y_{\text{trt}} - \bar{Y}_{\cdot \cdot})\) and \((Y - Y_{\text{trt}})\) are orthogonal.  Applying the Pythagorean theorem to the decomposition \(Y - \bar{Y}_{\cdot \cdot} = (Y - Y_{\text{trt}}) + (Y_{\text{trt}} - \bar{Y}_{\cdot \cdot})\) gives the sum of squares decomposition used above.

Tangent: \(R^2\) and F tests

In this section I discuss the relationship between the F statistic and \(R^2\), the coefficient of determination. The F statistic is a generalization of the t-test for an OLS slope, but does not fit into the “feature selection” narrative of the post.

The \(R^2\) is the fraction of variance explained by a linear model

\[R^2 = \frac{\text{SS}_{\text{reg}}}{SYY} = \frac{\text{SYY} - \text{RSS}}{\text{SYY}} = 1 - \frac{\text{RSS}}{\text{SYY}}.\]

The F statistic to test the fit of a multivariate linear model (compared to a simple intercept model) is:

\[\begin{aligned} F &= \frac{\text{SS}_{\text{reg}} / k}{\text{RSS} / (n-k-1)} \\ &= \frac{(\text{SYY} - \text{RSS}) / k}{\text{RSS} / (n-k-1)} \\ &= \left( \frac{n-k-1}{k} \right) \left( \frac{\text{SYY}}{\text{RSS}} - 1 \right). \end{aligned}\]

(See Geometric interpretations of linear regression and ANOVA for a discussion of the F statistic.)

We can write the F statistic as an increasing function of \(R^2 = 1 - \frac{\text{RSS}}{\text{SYY}}\):

\[F = \left( \frac{n-k-1}{k} \right) \left( \frac{R^2}{1-R^2} \right).\]

The \(R^2\) is expressable as the square correlation between predicted and observed values:

\[R^2 = \text{corr}\left(Y, \hat{Y} \right)^2.\]

It follows that an F-statistic p-value of a multivariate regression model is an increasing function of the absolute correlation between the observed values \(Y\) and the model’s predicted values \(\hat{Y}\).

References

Written on March 3rd , 2019 by Scott Roy
Feel free to share!

You may also enjoy: