statsandstuff a blog on statistics and machine learning
Implementing a neural network in Python
In this post, I walk through implementing a basic feed forward deep neural network in Python from scratch. See Introduction to neural networks for an overview of neural networks.
The post is organized as follows:
- Predictive modeling overview
- Training DNNs
- Stochastic gradient descent
- Forward propagation
- Back propagation
- Code
The Predictive modeling overview section discusses predictive modeling in general and how predictive models are fit. Deep neural networks are a type of predictive model and are fit like other predictive models. The section Training DNNs goes over computing derivatives of the loss function with respect to a DNN’s parameters. Finally the code is given in section Code.
Predictive modeling overview
A DNN is a type of predictive model and so before we discuss training DNNs in particular, let’s briefly go over what predictive models are and how they are fit. The basic task in predictive modelling is given data \((x^{(i)}, y^{(i)})\) consisting of features \(x^{(i)}\) and labels \(y^{(i)}\), ‘‘learn’’ a model function \(f\) such that \(y^{(i)} \approx f(x^{(i)})\). More precisely, we want the model that “best” satisfies \(f(x^{(i)}) \approx y^{(i)}\) for all training data \(i \in \{1, \ldots, N\}\), where best is defined with respect to a loss function. For each mistake where \(f(x^{(i)})\) is not \(y^{(i)}\), some loss \(\ell^{(i)}\) is incurred, e.g., \(\ell^{(i)} = ( f(x^{(i)}) - y^{(i)} )^2\) might be the square error. The average loss on the dataset is
\[\ell = (1 / N) (\ell^{(1)} + \ell^{(2)} + \ldots + \ell^{(N)}).\]Minimizing average loss on a particular dataset is usually not the goal (in fact, we can achieve zero loss by just “memorizing” the dataset). What we really care about solving is
\[\min_f \ \textbf{E}_{(x,y)}(\ell(f(x), y)),\]where the expectation is taken over the data distribution \((x, y)\). The optimal model is called the Bayes model and the corresponding loss is called the Bayes error. The Bayes error is a hard limit on how well we can predict a response \(y\) from features \(x\) with respect to a loss \(\ell\) and is usually unknown. For some tasks like object detection or speech recognition, the Bayes error is near zero because humans can do these tasks with near zero error. On the other hand, predicting if a borrower will default on a loan given a few characteristics like the loan amount, income, and credit score has a higher Bayes error. We can improve the Bayes error by using more informative features. (As an aside, for a regression problem with square loss, the Bayes regressor is the conditional expectation \(\textbf{E}(y \vert x)\) and the Bayes error is the conditional variance \(\textbf{Var}(y \vert x)\). Regression modeling therefore reduces to efficiently estimating/learning the conditional expectation.)
For tractability, most machine learning and statistics (including deep learning) is parametric. This means we restrict our model to lie in a parametrized class \(\mathcal{F} = \{ f_{\theta} : \theta \in \Theta\}\) (e.g., all linear functions or all neural networks of a given architecture). We also minimize loss over a sample of data. These simplifications lead to model class error and sample error:
-
Finding the best model in \(\mathcal{F}\) instead of the best model overall leads to model class error. Model class error can be improved by using a more complicated model class. Note that if a simple model already achieves loss close to the Bayes error, using a more complicated model won’t help much.
-
Training on a sample of data instead of an infinite population leads to sample error and jeopardizes generalizability. Sample error is usually addressed with training on more data or using regularization.
After these simplifications the learning problem is
\[\min_{\theta \in \Theta} J(\theta) := \frac{1}{N} \sum_{i=1}^N \ell^{(i)}(\theta) + R(\theta).\]Notice that the loss \(\ell^{(i)}(\theta)\) on the \(i\)th observation is a function of the model parameters (before the loss was a function of the model \(f\), but now \(f\) is identified with its parameters \(\theta\)). Also notice that we’ve included a regularization term \(R(\theta)\) to deal with sample error. The most common form of regularization is L2 regularization in which \(R(\theta) = \alpha \vert \vert \theta \vert \vert_2^2\).
Minimizing the regularized loss \(J\) over \(\theta\) may still be difficult. Optimization error occurs when we only find an approximate minimizer; this can be addressed by optimizing for more iterations (i.e., training for longer) or using a better optimization algorithm. The table below summarizes the different kinds of error in a predictive problem and how to improve each kind.
| Error | How to improve |
|---|---|
| Bayes error | Use better features |
| Model class error | Use a more complicated model |
| Sample error | Use regularization; get more data |
| Optimization error | Train longer; use a better optimization algorithm; reformulate loss/regularization to have properties more conducive to optimization like differentiability, Lipschitz continuous gradients, or strong convexity |
Before we discuss training DNNs, let’s quickly go over binary classification because it is formulated slightly differently than described above. In classification, the labels \(y^{(i)} \in \{0, 1\}\) indicate whether an event occurred or not (e.g., did a person default on their loan or did a user buy a product). Rather than model the labels \(y^{(i)}\) directly, the model returns \(p = f(x)\), the probability that \(y = 1\) (see ROC space and AUC for a discussion of the difference between a classifier and a scorer). In the classification setting, the loss is usually based on the likelihood of observing the training data under the model, assuming each observation is independent. For example, given outcomes \(y^{(1)} = 0\), \(y^{(2)} = 1\), and \(y^{(3)} = 0\) and model probabilities \(p^{(1)}\), \(p^{(2)}\), and \(p^{(3)}\), the likelihood of observing the data under the model is \(P = (1 - p^{(1)}) \cdot p^{(2)} \cdot (1 - p^{(3)})\). We define the loss as the negative log likelihood \(-\log P = -\log(1 - p^{(1)}) - \log p^{(2)} - \log(1 - p^{(3)})\). In general, the average negative log likelihood loss is
\[\ell = (1 / N) (\ell^{(1)} + \ldots + \ell^{(N)}),\]where \(\ell^{(i)} = -y^{(i)} \log p^{(i)} - (1 - y^{(i)}) \log(1 - p^{(i)})\). This is also called cross-entropy loss and is the most popular loss function for classification tasks. As above, the negative log likelihood is a function of the model parameters \(\theta\).
Training DNNs
In deep learning, as with general prediction tasks, the model fitting/learning involves minimizing the regularized loss function
\[J(\theta) = \ell(\theta) + R(\theta) = (1/N) \sum_{i=1}^N \ell^{(i)}(\theta) + R(\theta)\]over the parameters \(\theta\). This is often done with an iterative procedure such as gradient descent. In gradient descent, we initialize the parameters at some value and continuously move in the direction of the negative gradient:
- Initialize \(\theta = \theta_0\)
- Repeatedly update \(\theta = \theta - r (\nabla J)(\theta)\), where \(r\) is the step size or learning rate
The derivative is a linear operator so the gradient of \(J\) breaks apart:
\[\nabla J = \nabla \ell + \nabla R = (1/N) \sum_{i=1}^N \nabla \ell^{(i)} + \nabla R.\]The above expression shows why gradient descent can be prohibitively expensive in big data applications: each gradient computation requires computing \(\nabla \ell^{(i)}\) for every observation in the training data. The usual solution is to replace the gradient with a noisy, but cheap, stochastic approximation:
\[g = (1 / \vert B \vert) \sum_{i \in B} \nabla \ell^{(i)} + \nabla R,\]where \(B\) is a (random) batch of training data. This yields stochastic (or mini-batch) gradient descent.
(It is important that \(B\) is a random batch of training data so that \(\textbf{E}(g) = \nabla J\). This requires shuffling the training data before breaking it into batches.)
We have given all the details for training an arbitrary predictive model in a big data setting. In order to flesh out the details for deep learning, we just need to discuss how to compute \(\nabla \ell^{(i)}\), the derivative of the loss on a single training sample. Before discussing back propagation (the way we compute \(\nabla \ell^{(i)}\)), we discuss forward propagation as a way to introduce notation.
Forward propagation
Forward propagation is how we compute \(f(x)\), the network’s prediction for an observation with features \(x\). (In classification tasks, it’s how we compute \(p(x)\), the probability that \(y = 1\) given features \(x\).)
We let \(L\) denote the number of layers in the network and \(n_l\) denote the number of units in layer \(l\) for \(l \in \{0, 1, \ldots, L\}\). We let \(a^{[0](i)} = x^{(i)}\) be the input (for the \(i\)th data point), \(a^{[1](i)}\) be the activations from the first layer, \(a^{[2](i)}\) be the activations from the second layer, and so on. Notice that \(a^{[l](i)}\) is a vector of length \(n_l\). The output is \(f(x^{(i)}) = a^{[L](i)}\), the activations from the last layer. In a feed-forward network, the activations are defined recursively:
\[\begin{aligned} z^{[l](i)} &= W^{[l]} a^{[l-1](i)} + b^{[l]} \\ a^{[l](i)} &= g^{[l]}(z^{[l](i)}) \end{aligned}\]Here \(W^{[l]}\) is an \(n_l \times n_{l-1}\) matrix and \(b^{[l]}\) is an \(n_l \times 1\) vector that linearly transform the outputs \(a^{[l-1](i)}\) from the previous layer. The function \(g^{[l]}\) is a nonlinear activation function and is applied elementwise.
In code, we’ll process a batch of observations at a time. For simplicity, suppose our batch is the first \(m\) observations \(\{1, 2, \ldots, m\}\). For each observation \(i\) in the batch, we store \(z^{[l](i)}\) and \(a^{[l](i)}\) as columns in a matrix:
\[\begin{aligned} Z^{[l]} &= \begin{bmatrix} z^{[l](1)} & z^{[l](2)} & \ldots & z^{[l](m)} \end{bmatrix} \\ A^{[l]} &= \begin{bmatrix} a^{[l](1)} & a^{[l](2)} & \ldots & a^{[l](m)} \end{bmatrix} \end{aligned}\]With this notation, forward-propagating a batch requires recursively computing
\[\begin{aligned} Z^{[l]} &= W^{[l]} A^{[l-1]} + b^{[l]} \\ A^{[l]} &= g^{[l]}(Z^{[l]}), \end{aligned}\]where \(A^{[0]} = \begin{bmatrix} x^{(1)} & x^{(2)} & \ldots & x^{(m)} \end{bmatrix}\) is the matrix of input observations. (In computing \(Z^{[l]}\) above, \(W^{[l]} A^{[l-1]}\) is an \(n_l \times m\) matrix and \(b^{[l]}\) is an \(n_l \times 1\) vector. The addition is done with broadcasting (NumPy behavior), which adds \(b^{[l]}\) to each column of \(W^{[l]} A^{[l-1]}\).)
Back propagation
To train the network, we need to compute the derivative of the loss with respect to the network parameters \(\theta = (b^{[1]}, W^{[1]}, b^{[2]}, W^{[2]}, \ldots, b^{[L]}, W^{[L]})\). This is called back propagation, but is really just the chain rule.
As with forward propagation, we will start with the single observation case. Thinking recursively, suppose we already know
\[\frac{\partial \ell^{(i)}}{\partial a^{[l](i)}_j},\]the derivative of the loss on the \(i\)th observation for each unit \(j \in \{1, \ldots, n_l\}\) in the \(l\)th layer. Since we are limiting our discussion to a single observation, we’ll drop indexing by \(i\) from the notation and write:
\[\frac{\partial \ell^{(i)}}{\partial a^{[l]}_j}.\]We now discuss how to compute
- The derivative of the loss with respect to the parameters \(b^{[l]}\) and \(W^{[l]}\) in the \(l\)th layer.
- The derivative of the loss with respect to the previous layer’s units.
Parameter derivatives
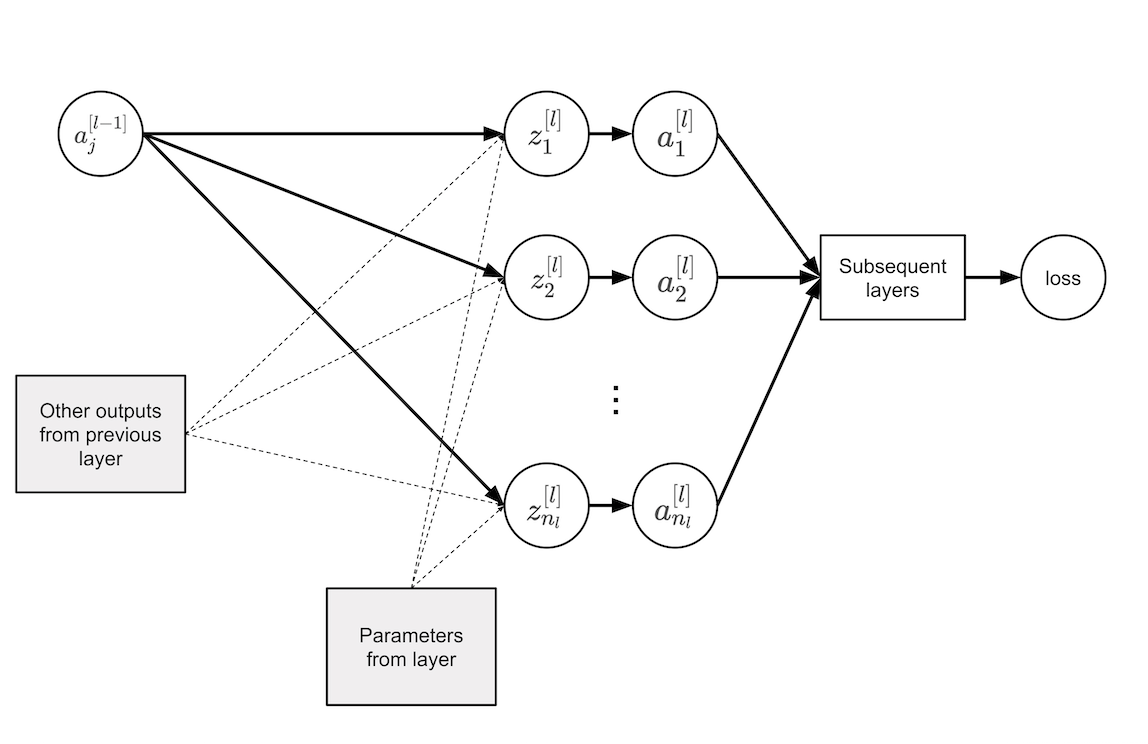
The figure below illustrates how the parameters in layer \(l\) affect the loss.
Since \(a_j^{[l]} = g^{[l]} ( z_j^{[l]} )\), the chain rule gives:
\[\begin{aligned} \frac{\partial \ell^{(i)}}{\partial z_j^{[l]}} &= \frac{\partial \ell^{(i)}}{\partial a_j^{[l]}}\frac{\partial a_j^{[l]}}{\partial z_j^{[l]}} \\ &= \frac{\partial \ell^{(i)}}{\partial a_j^{[l]}} \cdot (g^{[l]})'(z_j^{[l]}). \end{aligned}\]Putting these derivatives into a gradient vector, we have
\[\nabla_{z^{[l]}} \ell^{(i)} = \nabla_{a^{[l]}} \ell^{(i)} * (g^{[l]})'(z^{[l]}),\]where the \(*\) denotes elementwise multiplication and the function \((g^{[l]})'\) is applied elementwise.
The parameters \(b_j^{[l]}\) and \(W_{jk}^{[l]}\) affect the loss through \(z_j^{[l]}\) (see figure above). For \(b_j^{[l]}\), the chain rule gives:
\[\begin{aligned} \frac{\partial \ell^{(i)}}{\partial b_j^{[l]}} &= \frac{\partial \ell^{(i)}}{\partial z_j^{[l]}}\frac{\partial z_j^{[l]}}{\partial b_j^{[l]}} \\ &= \frac{\partial \ell^{(i)}}{\partial z_j^{[l]}} \cdot 1 \\ &= \frac{\partial \ell^{(i)}}{\partial z_j^{[l]}}. \end{aligned}\]This means \(\nabla_{b^{[l]}} \ell^{(i)} = \nabla_{z^{[l]}} \ell^{(i)}\).
Similarly for \(W_{jk}^{[l]}\):
\[\begin{aligned} \frac{\partial \ell^{(i)}}{\partial W_{jk}^{[l]}} &= \frac{\partial \ell^{(i)}}{\partial z_j^{[l]}} \frac{\partial z_j^{[l]}}{\partial W_{jk}^{[l]}} \\ &= \frac{\partial \ell^{(i)}}{\partial z_j^{[l]}} a_k^{[l-1]}. \end{aligned}\]Putting these derivatives into a gradient matrix, we have
\[\nabla_{W^{[l]}} \ell^{(i)} = \nabla_{z^{[l]}} \ell^{(i)} a^{[l-1]T}\](Recall that a column times a row is a matrix.)
Previous layer derivatives
The figure below shows how the previous layer \((l-1)\) affects the loss.
A particular unit \(a_j^{[l-1]}\) in the previous layer affects the loss through every unit in the current layer \(z_1^{[l]}, z_2^{[l]}, \ldots, z_{n_l}^{[l]}\).
The multivariate chain rule therefore gives
\[\begin{aligned} \frac{\partial \ell^{(i)}}{\partial a_j^{[l-1]}} &= \frac{\partial \ell^{(i)}}{\partial z_1^{[l]}} \frac{\partial z_1^{[l]}}{\partial a_j^{[l-1]}} + \frac{\partial \ell^{(i)}}{\partial z_2^{[l]}} \frac{\partial z_2^{[l]}}{\partial a_j^{[l-1]}} + \ldots + \frac{\partial \ell^{(i)}}{\partial z_{n_l}^{[l]}} \frac{\partial z_{n_l}^{[l]}}{\partial a_j^{[l-1]}} \\ &= \frac{\partial \ell^{(i)}}{\partial z_1^{[l]}} W_{1j}^{[l]} + \frac{\partial \ell^{(i)}}{\partial z_2^{[l]}} W_{2j}^{[l]} + \ldots + \frac{\partial \ell^{(i)}}{\partial z_{n_l}^{[l]}} W_{n_lj}^{[l]} \end{aligned}\]Putting these in a vector, we have
\[\nabla_{a^{[l-1]}} \ell^{(i)} = W^{[l]T} \nabla_{z^{[l]}} \ell^{(i)}\]Back propagation on a batch
Summarizing the derivatives from the previous sections, for a single observation we have:
\[\begin{aligned} \nabla_{z^{[l]}} \ell^{(i)} &= \nabla_{a^{[l]}} \ell^{(i)} * (g^{[l]})'(z^{[l]}) \\ \nabla_{b^{[l]}} \ell^{(i)} &= \nabla_{z^{[l]}} \ell^{(i)} \\ \nabla_{W^{[l]}} \ell^{(i)} &= \nabla_{z^{[l]}} \ell^{(i)} a^{[l-1]T} \\ \nabla_{a^{[l-1]}} \ell^{(i)} &= W^{[l]T} \nabla_{z^{[l]}} \ell^{(i)}. \end{aligned}\]As before, we consider a batch consisting of the first \(m\) observations and let \(Z^{[l]}\) and \(A^{[l]}\) be matrices whose \(i\)th columns are the network values in layer \(l\) evaluated on the \(i\)th observation.
We also let
\[\begin{aligned} dZ^{[l]} = \begin{bmatrix} \nabla_{z^{[l](1)}} \ell^{(1)} & \nabla_{z^{[l](2)}} \ell^{(2)} & \ldots & \nabla_{z^{[l](m)}} \ell^{(m)} \end{bmatrix} \\ dA^{[l]} = \begin{bmatrix} \nabla_{a^{[l](1)}} \ell^{(1)} & \nabla_{a^{[l](2)}} \ell^{(2)} & \ldots & \nabla_{a^{[l](m)}} \ell^{(m)} \end{bmatrix} \end{aligned}\]be a matrices of gradients. Notice that each column is a gradient of a different function \(\ell^{(i)}\).
From the single observation case and the definitions of \(dZ^{[l]}\) and \(dA^{[l]}\), it is immediately clear that
\[\begin{aligned} dZ^{[l]} &= dA^{[l]} * (g^{[l]})'(Z^{[l]}) \\ dA^{[l-1]} &= W^{[l]T} dZ^{[l]}. \end{aligned}\]For the parameters \(b^{[l]}\) and \(W^{[l]}\), we are interested in the derivatives of the average batch loss \(\ell^{\text{batch}} = \frac{1}{m} (\ell^{(1)} + \ldots + \ell^{(m)})\):
\[\begin{aligned} \nabla_{b^{[l]}} \ell^{\text{batch}} &= \frac{1}{m} \text{rowSum}\left( dZ^{[l]} \right) \\ \nabla_{W^{[l]}} \ell^{\text{batch}} &= \frac{1}{m} dZ^{[l]} A^{[l-1]T}. \end{aligned}\](To see the second equation, consider writing the matrix multiplication as an outer product expansion.) Summarizing the batch back propagation equations, we have:
\[\begin{aligned} dZ^{[l]} &= dA^{[l]} * (g^{[l]})'(Z^{[l]}) \\ dA^{[l-1]} &= W^{[l]T} dZ^{[l]} \\ \nabla_{b^{[l]}} \ell^{\text{batch}} &= \frac{1}{m} \text{rowSum}\left( dZ^{[l]} \right) \\ \nabla_{W^{[l]}} \ell^{\text{batch}} &= \frac{1}{m} dZ^{[l]} A^{[l-1]T}. \end{aligned}\]Code
This section goes over implementing a neural network in Python/NumPy. The code is fairly comprehensive, but is intended for pedagogical (not production) purposes. As such, things like error checking and unit tests (e.g., gradient checking with finite differences) are not implemented. The code supports
- Arbitrary feed forward architectures
- Input normalization
- Arbitrary loss and activation functions
- Batch gradient descent
- L2 regularization
The code does not support:
- Batch normalization
- Momentum
- Adam
- Dropout
- Normalizing input in a streaming fashion (as opposed to computing
muandsigover the entire dataset) - Automatric learning rate decay and early stopping using a validation set
Activation functions
An activation function has a signature like
def activationFunction(x, return_derivative=True)
and returns a dict with keys value and derivative (if returned). The input x is a numpy array. The outputs value and derivative are also numpy arrays with the same shape as x. Below are implementations of some common activation functions.
def tanh(x, return_derivative=True):
r = dict()
a = np.tanh(x)
r["value"] = a
if return_derivative:
g = 1 - np.power(a, 2)
r["derivative"] = g
return r
def sigmoid(x, return_derivative=True):
r = dict()
a = 1 / (1 + np.exp(-x))
r["value"] = a
if return_derivative:
g = a * (1 - a)
r["derivative"] = g
return r
def relu(x, return_derivative=True):
r = dict()
a = np.maximum(x, 0.0)
r["value"] = a
if return_derivative:
g = (x >= 0).astype(float)
r["derivative"] = g
return r
def linear(x, return_derivative=True):
r = dict()
a = x
r["value"] = a
if return_derivative:
g = np.ones(a.shape)
r["derivative"] = g
return r
Loss functions
A loss function has signature like
def lossFunction(A, Y, return_derivative=True).
The inputs A (predictions) and Y (labels) are numpy arrays of the same shape. The output is a dictionary with keys value and derivative (if returned), both of which are numpy arrays of the same shape as the two inputs A and Y. The array derivative must be the derivative of the loss function with respect to the predictions A.
The cross-entropy and square loss functions are implemented below. The cross-entropy loss below does not properly handle edge cases when \(A = \pm 1\), which should be corrected before productionizing the code.
def xent(A, Y, return_derivative=True):
r = dict()
l = -(Y * np.log(A) + (1-Y) * np.log(1 - A))
r["value"] = l
if return_derivative:
dA = -(Y / A - (1 - Y) / (1 - A))
r["derivative"] = dA
return r
def square(A, Y, return_derivative=True):
r = dict()
l = (Y - A)**2
r["value"] = l
if return_derivative:
dA = -2 * (Y - A)
r["derivative"] = dA
return r
DNN class
Below is an implementation of a DNN class. The code is self-explanatory. Backpropagation is the most complicated method and uses the equations we derived in previous sections.
class DNN(object):
def __init__(self, input_size, layer_sizes, activation_functions, loss):
self.nlayers = len(layer_sizes)
self.input_size = input_size
self.layer_sizes = layer_sizes
# In many cases, it's useful to view the input as the "zeroth" layer.
# We define a private variable _layer_sizes for this.
self._layer_sizes = [input_size]
self._layer_sizes.extend(layer_sizes)
self.activation_functions = activation_functions
self.loss = loss
def _initialize_parameters(self):
# Similar to Xavier initialization, but is adapted for RELU
self.params = dict()
for l in range(1, len(self._layer_sizes)):
self.params["W" + str(l)] = np.sqrt(2 / self._layer_sizes[l-1]) * np.random.randn(self._layer_sizes[l], self._layer_sizes[l-1])
self.params["b" + str(l)] = np.zeros((self._layer_sizes[l], 1))
def _loss_lookup(self, name):
if name == "xent":
return xent
elif name == "square":
return square
else:
raise Exception(name + " is not an implemented loss function.")
def _activation_lookup(self, name):
if name == "tanh":
return tanh
elif name == "sigmoid":
return sigmoid
elif name == "relu":
return relu
elif name == "linear":
return linear
else:
raise Exception(name + " is not an implemented activation function.")
def _forward_propagate(self, X, params, return_cache=False):
cache = dict()
A = X
if return_cache:
cache["A0"] = A
for l in range(1, self.nlayers + 1):
Z = np.dot(params["W" + str(l)], A) + params["b" + str(l)]
g = self._activation_lookup(self.activation_functions[l-1])(Z, return_derivative=return_cache)
A = g["value"]
if return_cache:
cache["A" + str(l)] = A
cache["gPrime" + str(l)] = g["derivative"]
if return_cache:
return A, cache
return A
def _back_propagate(self, X, Y, params, cache):
grads = dict()
m = X.shape[1]
A = cache["A" + str(self.nlayers)]
r = self._loss_lookup(self.loss)(A, Y, return_derivative=True)
grads["dA" + str(self.nlayers)] = r["derivative"]
loss = (1 / m) * np.sum(r["value"])
for l in range(self.nlayers, 0, -1):
grads["dZ" + str(l)] = grads["dA" + str(l)] * cache["gPrime" + str(l)]
grads["dA" + str(l-1)] = np.dot(self.params["W" + str(l)].T, grads["dZ" + str(l)])
grads["dByW" + str(l)] = (1 / m) * np.dot(grads["dZ" + str(l)], cache["A" + str(l-1)].T)
grads["dByb" + str(l)] = (1 / m) * np.sum(grads["dZ" + str(l)], axis=1, keepdims=True)
return grads, loss
def _update_parameters(self, params, grads, learning_rate = 0.1, l2_regularization = 0.0):
for l in range(1, self.nlayers + 1):
params["W" + str(l)] -= learning_rate * (grads["dByW" + str(l)] + l2_regularization * params["W" + str(l)])
params["b" + str(l)] -= learning_rate * (grads["dByb" + str(l)] + l2_regularization * params["b" + str(l)])
return params
def train(self, X, Y, batch_size=32, n_epochs=10, learning_rate=0.1, l2_regularization=0.01, verbose=True):
# Normalize input
self.mu = np.mean(X, axis=1, keepdims=True)
self.sig = np.std(X, axis=1, keepdims=True)
X_std = (X - self.mu) / self.sig
# Initialize parameters
self._initialize_parameters()
losses = []
n_obs = X.shape[1]
n_full_batches = int(n_obs / batch_size)
last_batch_size = n_obs - batch_size * n_full_batches
for epoch in range(n_epochs):
# Shuffle data
order = np.random.permutation(n_obs)
for batch in range(n_full_batches):
# Define batch
batch_ind = order[(batch * batch_size):((batch + 1) * batch_size)]
X_batch_std = X_std[:, batch_ind]
Y_batch = Y[:, batch_ind]
# Forward/back propagate to compute parameter gradients
A, cache = self._forward_propagate(X_batch_std, self.params, return_cache=True)
grads, loss = self._back_propagate(X_batch_std, Y_batch, self.params, cache)
# Update parameters
self.params = self._update_parameters(self.params, grads, learning_rate, l2_regularization)
losses.append(loss)
if verbose and (batch % 100 == 0):
print("Loss after epoch " + str(epoch) + " batch " + str(batch) + ": " + str(loss))
if last_batch_size > 0:
# Define batch
batch_ind = order[(n_full_batches * batch_size):]
X_batch_std = X_std[:, batch_ind]
Y_batch = Y[:, batch_ind]
A, cache = self._forward_propagate(X_batch_std, self.params, return_cache=True)
grads, loss = self._back_propagate(X_batch_std, Y_batch, self.params, cache)
self.params = self._update_parameters(self.params, grads, learning_rate, l2_regularization)
losses.append(loss)
if verbose and (batch % 100 == 0):
print("Loss after epoch " + str(epoch) + " batch " + str(batch) + ": " + str(loss))
return losses
def predict(self, X):
X_std = (X - self.mu) / self.sig
A = self._forward_propagate(X_std, self.params, return_cache=False)
return A
Toy data
To test the DNN class, we define a toy dataset below.
n = 2
m = 100000
v1 = np.random.randn(n,1)
v2 = np.random.randn(n,1)
X_train = np.random.randn(n,m)
Y_train = np.minimum((np.dot(v1.T, X_train) > 0).astype(float) + (np.dot(v2.T, X_train) > 0).astype(float), 1)
X_test = np.random.randn(n,m)
Y_test = np.minimum((np.dot(v1.T, X_test) > 0).astype(float) + (np.dot(v2.T, X_test) > 0).astype(float), 1)
The classes are not linearly separable so logistic regression will not work very well (see plot of test data below).

Train a DNN on toy data
Below we use our DNN class to define a network architecture and train it on the toy data.
input_size = n
layer_sizes = [8, 4, 1]
activation_functions = ["relu", "relu", "sigmoid"]
loss = "xent"
dnn = DNN(input_size, layer_sizes, activation_functions, loss)
dnn.train(X_train, Y_train, batch_size=64, n_epochs=20, learning_rate=0.01, l2_regularization=0.01)
The classifier achieves 98% accuracy on the test data, which we compute with the following code:
A = dnn.predict(X_test)
np.mean((A > 0.5).astype(float) == Y_test)