Calibration in logistic regression and other generalized linear models

In general, scores returned by machine learning models are not necessarily well-calibrated probabilities (see my post on ROC space and AUC).  The probability estimates from a logistic regression model (without regularization) are partially calibrated, though.  In fact, many generalized linear models, including linear regression, logistic regression, binomial regression, and Poisson regression, give calibrated predicted values.

Where calibrated models are important?

Before delving deeper into why most generalized linear models give calibrated estimates, let’s consider a situation in which calibrated estimates are important.  In online advertising, such as on Google or Facebook, an advertiser pays the ad company only when a user clicks on an ad (they are not charged just to show the ad).  An important task for the ad company is to decide which ads to show in its limited ad space.  Simply showing the ad with the highest bid will not maximize the ad company’s revenue.  For example, suppose that advertiser A has bid $10 for every click and advertiser B has bid $1 for every click.  Although advertiser B has bid less, suppose its ad is 20 times more likely to be clicked on.  In this case, the ad company will make twice as much money showing advertiser B’s ad (even though advertiser A has bid 10 times as much per click).  When deciding which ads to show, the ad company must consider two factors: 1) how much the advertiser has bid to pay the ad company each time its ad is clicked and 2) how likely a user is to click on the ad.  Inaccurately predicting how likely a user is to click on an ad may cause the ad company to make a suboptimal decision in which ad to show.  Logistic regression, discussed next, is very popular in online advertising.

Logistic regression

In the logistic regression model, each unit of observation \(i\) has a binary response \(y_i \in \{ 0, 1\}\), where the probability \(p_i\) that \(y_i = 1\) depends on some features \(X_i\) of the unit.  The units are assumed independent, but they are not i.i.d. since the probability that the response \(y_i\) is 1 varies for each unit, depending on its features \(X_i\).  The units are linked by assuming that \(p_i\) has a specific parametric form, with shared parameters \(\beta\) across all units.  In particular, the log-odds \(\log \left( \frac{p_i}{1-p_i} \right)\) is assumed a linear function of the predictors with coefficients \(\beta\):

\[\log \left( \frac{p_i}{1-p_i} \right) = \beta^T X_i = \beta_1 X_{i1} + \beta_2 X_{i2} + \ldots \beta_p X_{ip}.\]

The log-odds function is also called the logit function \(\text{logit}(p) = \log \left( \frac{p}{1-p} \right)\).

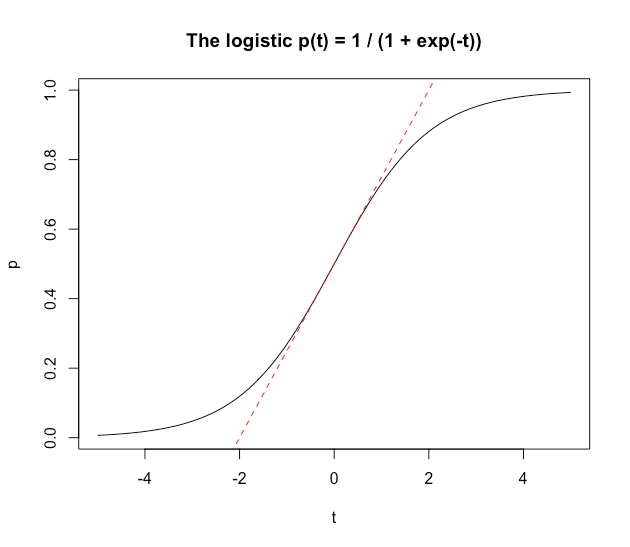
By inverting the logit, we get the parametric form for the probabilities: \(p_i = \text{logit}^{-1}(p_i) = \frac{1}{1 + e^{-\beta^T X_i}}\).  The inverse of the logit is called the logistic function (logistic regression is so-named because it models probabilities with a logistic function).  The estimates in logistic regression are harder to interpret than those in linear regression because increasing a predictor by 1 does not change the probability of outcome by a fixed amount.  This is because the logistic function \(p(t) = \frac{1}{1 + e^{-t}}\) is not a straight line (see the graph below).  Nevertheless, the logistic is nearly linear for values of \(t\) between -1 and 1, which corresponds to probabilities between 0.27 and 0.73 (see dashed red line in figure).  The slope of the dashed red line is 1/4 (the derivative of the logistic at \(t = 0\)).  For a moderate range of probabilities (about 0.3 to 0.7), increasing the covariate \(X_{ij}\) by 1 will change the predicted probability by about \(\frac{\beta_j}{4}\) (increase or decrease, depending on the sign of \(\beta_j\)).  Since the red line is the steepest part of the logistic curve, the approximated change \(\frac{\beta_j}{4}\) is always an upper bound (even for probabilities outside the range 0.3 to 0.7).

Fitting logistic regression and calibration

Logistic regression is fit with maximum likelihood estimation.  The likelihood is

\[L(\beta) = \prod_{i=1}^n p_i^{y_i} (1-p_i)^{1-y_i}\]

and the negative log-likelihood is

\[l(\beta) = \sum_{i=1}^n -y_i \log p_i - (1-y_i) \log (1 - p_i).\]

Taking a derivative with respect to \(\beta\) (using the fact that \(\nabla_{\beta}\ -\log p_i = -(1-p_i) X_i\) and \(\nabla_{\beta} -\log(1-p_i) = p_i X_i\)), we get

\[\nabla l(\beta) = \sum_{i=1}^n -(1-p_i) y_i X_i + p_i (1-y_i) X_i = \sum_{i=1}^n -y_i X_i + p_i X_i.\]

The probabilities thus satisfy

\[\sum_{i=1}^n y_i X_i = \sum_{i=1}^n p_i X_i.\]

These are calibration equations.  They hold for each component of the covariate vector \(X_i = (X_{i1}, X_{i2}, \ldots, X_{ip})\):

\[\sum_{i=1}^n y_i X_{ij} = \sum_{i=1}^n p_i X_{ij}.\]

Under the logistic model, \(p_i = \text{E}(y_i)\) and so the above equations say that the observed value of \(\sum_{i=1}^n y_i X_{ij}\) in the data equals its expected value, according to the MLE fitted model.  Since \(y_i \in \{0, 1\}\), these equations further simplify to: the observed sum of a covariate over the positive class equals the expected sum of the covariate over the positive class.

To explain how these equations calibrate the model, let’s walk through an example.  Suppose we are predicting whether an English major is a man or women using 3 predictors: an intercept, an indicator for whether the student likes Jane Austen, and height.  Let \(p_i\) be the probability that student \(i\) is a man.  The calibration equations say:

1. (Intercept equation) The number of male English majors in the data equals \(\sum_{i=1}^n p_i\), the expected number of male English majors in the data, as predicted by the logistic model.
2. (Jane Austen equation) The number of male English majors who like Jane Austen in the data equals \(\sum_{i \text{ likes Jane Austen}} p_i\), the expected number of male English majors who like Jane Austen in the data, as predicted by the logistic model.
3. (Height equation) The sum of heights of all men in the data equals \(\sum_{i=1}^n \text{height}_i \cdot p_i\), the expected sum of heights of all men in the data, as predicted by the model.  Combined with the first equation, we could reword this as: the average height of a man in the data equals the expected height of a man, as predicted by the model.

Note: the calibration equations have many solutions for the probabilities.  Logistic regression chooses the solution of the form \(p_i = \frac{1}{1 + e^{-\beta^T X_i}}\).

How does up and down sampling change \(\text{P}(y \vert x)\)?

Suppose we downsample the positive class by keeping only 10% of its observations. This changes \(P(y \vert x)\) and therefore the scores from an ML model. To see how the scores change, assume the \(y\) conditional on \(x\) follows some distribution \(\text{P}(y \vert x)\) before downsampling. We are then interested in the distribution of \(y\) conditional on \(x\) and the data being kept, i.e., the distribution \(\text{P}(y \vert x, \text{ keep})\). Using Bayes, we can write this as

\[\text{P}(y \vert x, \text{ keep}) = \frac{\text{P}(\text{keep} \vert y, x) \text{P}(y \vert x)}{\text{P}(\text{keep} \vert x)}.\]

If the positive class is kept with probability \(\alpha\) and the negative class is not downsampled, we have

\[\begin{aligned} \text{P}(\text{keep} \vert y=1, x) &= \alpha, \\ \text{P}(\text{keep} \vert y=0, x) &= 1, \text{ and} \\ \text{P}(\text{keep} \vert x) &= \alpha \text{P}(y = 1 \vert x) + \text{P}(y = 0 \vert x). \end{aligned}\]

Plugging these into the expression for \(\text{P}(y \vert x, \text{ keep})\), and letting \(p(x) := \text{P}(y = 1 \vert x)\) for brevity, we have

\[\text{P}(y = 1 \vert x, \text{ keep}) = \frac{\alpha p(x)}{\alpha p(x) + 1-p(x)}.\]

Notice that \(p \mapsto \alpha p / (\alpha p + 1 - p)\) is increasing in \(p\), which means the scores from the model trained on the downsampled data have the same ordering as the scores from the model trained on the original data. The AUC, which only depends on the score order, also does not change. (There may be slight fluctuations in the scores/AUC after downsampling due to estimation errors in finite samples.)

The odds after downsampling are just multipled by \(\alpha\)

\[\text{odds}(y = 1 \vert x, \text{ keep}) := \frac{\text{P}(y=1 \vert x, \text{ keep})}{\text{P}(y=0 \vert x, \text{ keep})} = \alpha \cdot \text{odds}(y = 1 \vert x),\]

and the log odds are shifted by \(\log(\alpha)\). It follows that downsampling only shifts the intercept term in logistic regression by \(\log(\alpha)\) and the other terms are unaffected (in the infinite data setting).

How downsampling changes the decision boundary?

The decision boundary in a classificaiton task is shifted after downsampling. Suppose we set the decision boundary at odds 1, which corresponds to score 0.5. This boundary on the scores of the model trained on downsampled data corresponds to an odds boundary of \(1 / \alpha\) on the scores from the model trained on the original data. If \(\alpha\) is chosen to balance the classes, the score threshold 0.5 on the balanced data is equivalent to using score threshold equal to the prevalence of the majority class on the original data.

How does stratified sampling change \(\text{P}(y \vert x)\)?

Downsampling data by keeping observations with some probability based on \(y\) changes \(\text{P}(y \vert x)\), but in a predictable way. If we instead downsample by keeping observations with some probability based on \(x\), \(\text{P}(y \vert x)\) is unchanged. This is easy to see from the above equation for \(\text{P}(y \vert x, \text{ keep})\). Since observations are kept based on \(x\), it follows that \(\text{P}(\text{keep} \vert y, x) = \text{P}(\text{keep} \vert x)\) and so \(\text{P}(y \vert x, \text{ keep}) = \text{P}(y \vert x)\). Stratified sampling is a particular example of this.

To make this concrete, suppose our observations are people and the binary covariates age and gender split the data into four groups: young men, old men, young women, and old women. Moreover, suppose the prevalences of those groups are 20%, 40%, 30%, and 10%, respectively. We can create a new dataset in which all four groups are equally represented by downsampling the first group with fraction \(\alpha_1 = 1/2\), the second group with \(\alpha_2 = 1/4\), the third group with \(\alpha_3 = \frac{1}{3}\), and the fourth group with \(\alpha_4 = 1\). The conditional probabilities \(\text{P}(y \vert x)\) on this new balanced dataset are unchanged. (We do run into issues if \(\text{P}(x) > 0\) in the original dataset, but \(\text{P}(x) = 0\) in the new dataset.) Although downsampling data does not change our estimate means, it does change the variance and statistical uncertainty.

Binomial regression

Binomial regression is a generalization of logistic regression.  In binomial regression, each response \(y_i\) is the number of successes in \(n_i\) trials, where the probability of success is \(p_i\) is modeled with the logistic function:

\[p_i = \frac{1}{1 + e^{-\beta^T X_i}}.\]

The only change from logistic regression is that the likelihood (up to a constant factor independent of \(\beta\)) is now :

\[L(\beta) \propto \prod_{i=1}^n p_i^{y_i} (1-p_i)^{n_i-y_i}.\]

Working through the derivatives, the MLE estimates for \(p_i\) satisfy:

\[\sum_{i=1}^n y_i X_i = \sum_{i=1}^n n_i p_i X_i.\]

Notice that \(n_i p_i\) is the expected value of \(y_i\) under the model.  These are the same calibration equations from logistic regression.

Note: logistic regression is a special case of binomial regression where \(n_i = 1\) for all units.  Similarly, binomial regression is equivalent to a logistic regression where the response \(1\) and the predictor \(X_i\) is repeated \(y_i\) times in the data matrix, and the response \(0\) and the predictor \(X_i\) is repeated \(n_i - y_i\) times.

Linear regression

The regression equations are \(X^T X \beta = X^T Y\) (see Geometric interpretations of linear regression and ANOVA for more about the geometry behind these equations).  The predicted value in regression is \(\hat{Y} = X \hat{\beta}\), where \(\hat{\beta}\) solves the regression equations.  Thus, the regression equations say that \(X^T \hat{Y} = X^T Y\) or \(\sum_{i=1}^n \hat{y}_i X_i = \sum_{i=1}^n y_i X_i\).  Again, these are the calibration equations from above.  Note that \(\hat{y}_i\) is the mean of \(y_i\) under the linear regression model.

Poisson regression

In Poission regression, the response \(y_i\) is a Poisson random variable with rate \(\lambda_i\) (\(\lambda_i\) is also the mean and variance).  The rates across different units are linked by assuming that the log-rate is a linear function of the predictors \(X_i\) with common slope \(\beta\): \(\log \lambda_i = \beta^T X_i\).  Often Poisson regression includes an exposure term \(u_i\) so that \(\lambda_i\) is the rate per unit of exposure.  In other words, unit \(i\) has response that is modeled Poisson with rate \(u_i \lambda_i\).  The log-rate is \(\log(u_i) + \log(\lambda_i) = \log(u_i) + \beta^T X_i\).  The exposure term \(\log(u_i)\) is called the offset and is constrained to have coefficient \(1\) in the fitting process.

In Poisson regression, the likelihood is

\[L(\beta) = \prod_{i=1}^n \frac{e^{-\lambda_i} \lambda_i^{y_i}}{y_i!},\]

and the negative log-likelihood (up to a constant) is

\[l(\beta) =  \sum_{i=1}^n \lambda_i - y_i \log \lambda_i.\]

Differentiating with respect to \(\beta\), we see that the fitted rates satisfy the calibration equations:

\[\sum_{i=1}^n \lambda_i X_i = \sum_{i=1}^n y_i X_i\]

Exponential family with canonical link function

The calibration equations hold for any generalized linear model with “canonical” link function.  A random variable \(Y\) follows follows a scalar exponential family distribution if its density is of the form

\[f(y) = a(\theta) b(y) e^{\theta y},\]

where \(a(\theta) > 0\) and \(b(y) \geq 0\).  In other words, the parameter \(\theta\) and \(y\) only occur together as a product in an exponential.  The mean of an exponential family random variable can be expressed in terms of \(a(\theta)\):

\[E(y) = -\frac{a'(\theta)}{a(\theta)} = - \frac{\text{d}}{\text{d} \theta} \log a(\theta).\]

To see this, differentiate the density in \(\theta\)

\[\begin{aligned} \frac{\text{d}}{\text{d} \theta} \ f(y) &=  a'(\theta) b(y) e^{\theta y} + a(\theta) b(y) e^{\theta y} y \\ &= \frac{a'(\theta)}{a(\theta)} f(y) + y f(y) \end{aligned}\]

and then integrate over \(y\) (or sum if \(Y\) is discrete):

\[\int_{y} \frac{\text{d}}{\text{d} \theta}\ f(y) = \frac{a'(\theta)}{a(\theta)} + \text{E} \left( y \right).\]

By interchanging the derivative and the integral, we see that this quantity is also 0:

\[\int_{y} \frac{\text{d}}{\text{d} \theta}\ f(y) = \frac{\text{d}}{\text{d} \theta} \int_{y} f(y) = \frac{\text{d}}{\text{d} \theta} 1 = 0.\]

To make the concept of an exponential family more concrete, let’s see why the binomial distribution (with fixed number of trials \(n\)) is an exponential family:

\[\binom{n}{y} p^y (1-p)^{n-y} = \binom{n}{y} (1-p)^n e^{\log \left( \frac{p}{1-p} \right) \cdot y }.\]

In this case, the natural parameter is \(\theta = \log \left( \frac{p}{1-p} \right)\).  The binomial distribution is not an exponential family random variable if the number of trials \(n\) is considered a parameter (because then the range of \(Y\) depends on the parameter \(n\), which means that \(\theta\) and \(y\) are coupled outside the exponential).

Suppose that the response \(y_i\) of unit \(i\) has exponential family distribution with natural parameter \(\theta_i\).  Suppose further that the parameters are related by \(\theta_i = \beta^T X_i\), where \(X_i\) is a covariate vector for unit \(i\).

The negative log-likelihood (up to a constant in \(\beta\)) is

\[l(\beta) = \sum_{i=1}^n -\log a(\theta_i) - \theta_i y_i.\]

Differentiating in \(\beta\) (to find the MLE), we get

\[\sum_{i=1}^n \text{E} \left( y_i \right) X_i - y_i X_i.\]

The expected values \(\text{E}(y_i)\) from the MLE fitted model therefore satisfy the calibration equations:

\[\sum_{i=1}^n \text{E} \left( y_i \right) X_i = \sum_{i=1}^n y_i X_i.\] Written on August 21st , 2018 by Scott Roy