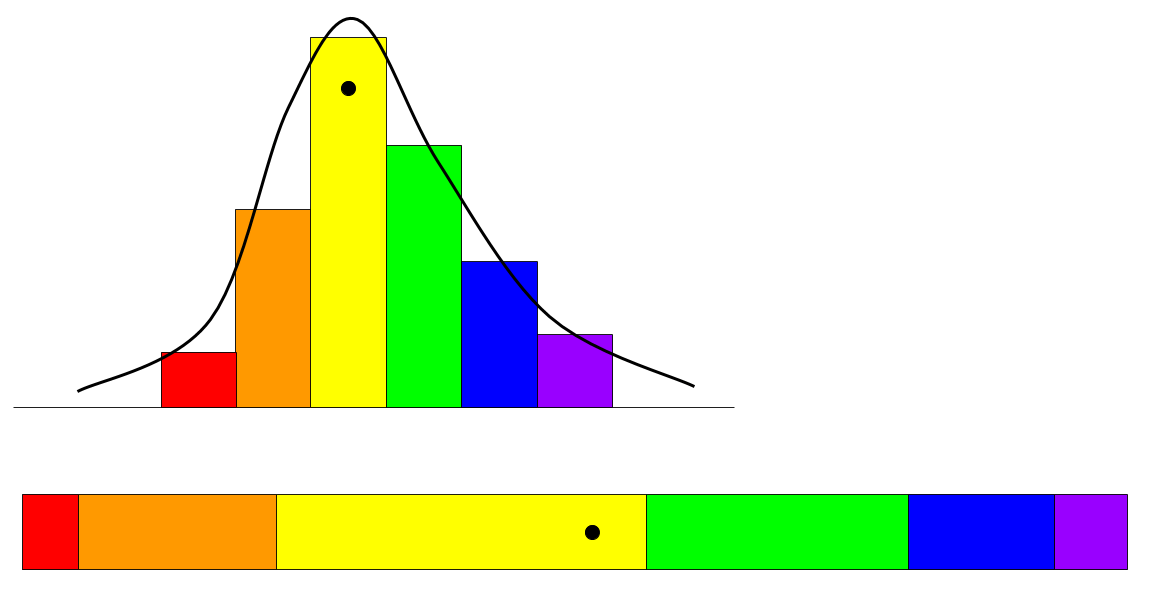
Sampling from distributions

There is almost no difference between knowing a distribution’s density (and thus knowing its mean, variance, mode, or anything else about it) and being able to sample from the distribution. On the one hand, if we can sample from a distribution, we can estimate the density with a histogram or kernel density estimator. Conversely, I’ll discuss w... Read more 12 May 2018 - 6 minute read

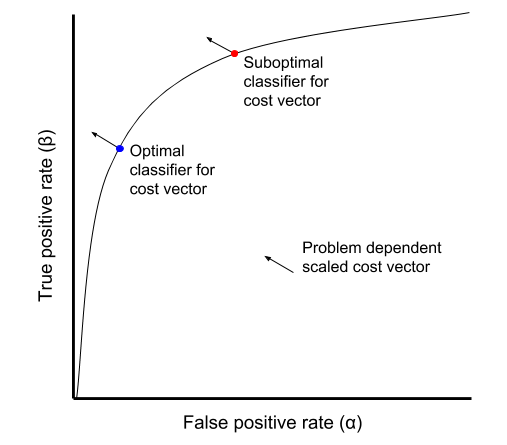
ROC space and AUC

Before discussing ROC curves and AUC, let’s fix some terminology around the confusion matrix: Condition positive (negative): real positive (negative) case in the data True positive (negative): condition positive (negative) that is classified as positive (negative) False positive (negative): condition negative (positive) that is classifie... Read more 29 Apr 2018 - 7 minute read

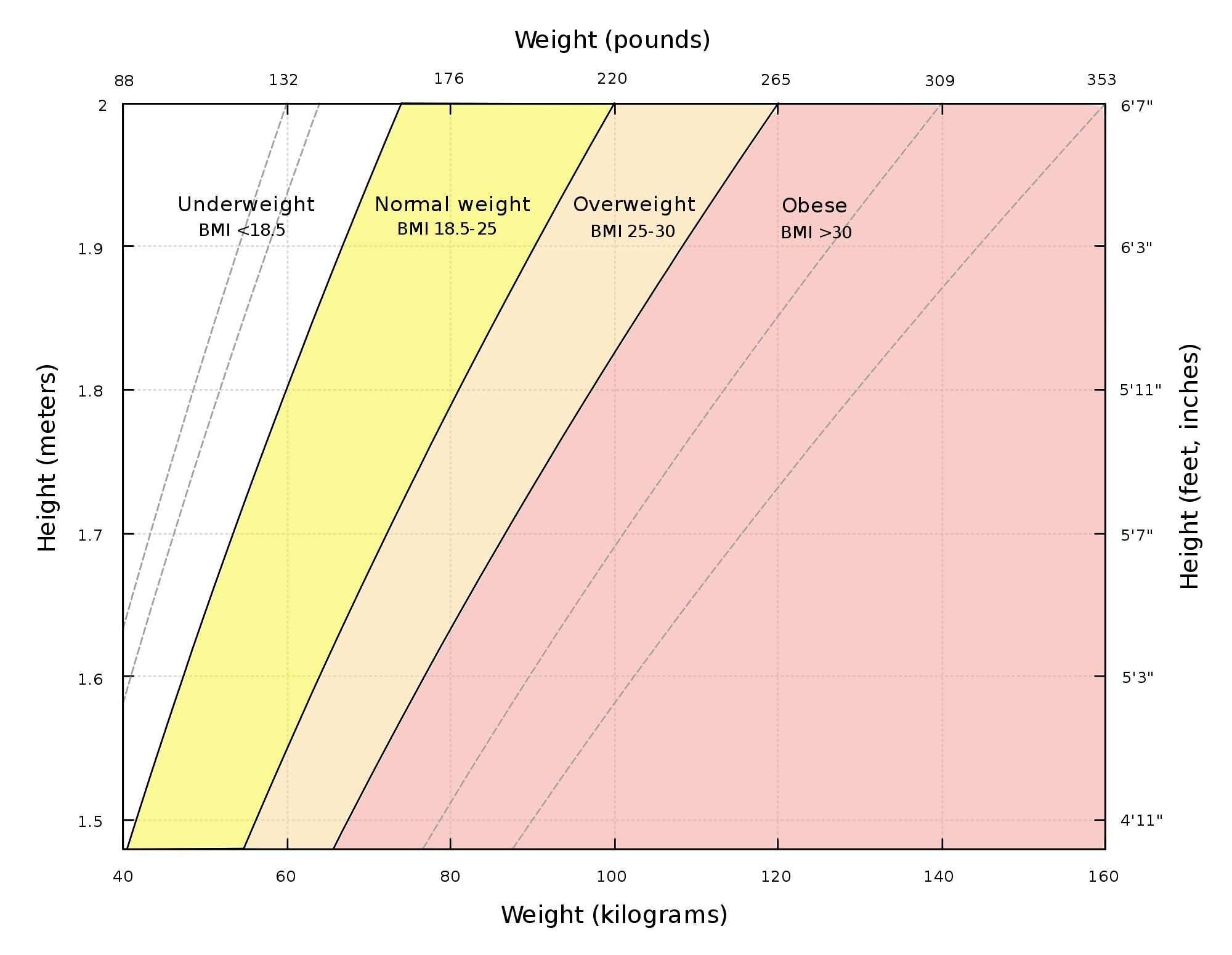
Propagation of error

Propagation of error describes how uncertainty in estimates propagates forward when we consider functions of those estimates. Suppose I have height and weight measurements for a sample of people. What is the mean and variance of the BMI? (BMI is 703 times the weight (in pounds) over the square of the height (in inches).) The obvious thing is... Read more 28 Apr 2018 - 3 minute read

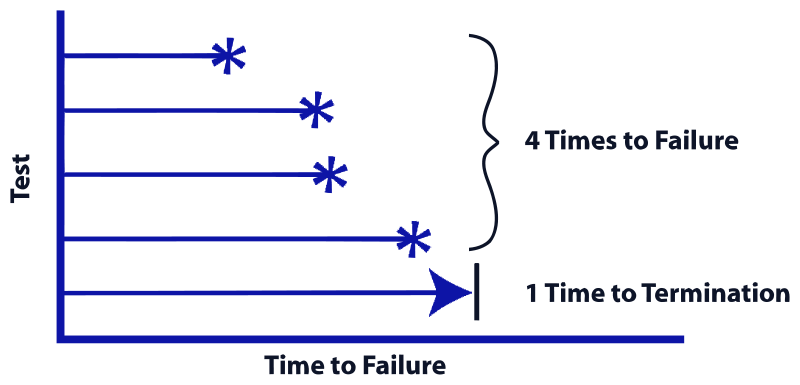
Maximum likelihood estimation with censored data

Suppose I’m tasked with analyzing failure times for hard drives in a datacenter. I track 100 hard drives over a 2 year period, and if a hard drive fails, I record when. If the hard drive has not failed by the 2 year mark, I don’t when when it will fail, just that its failure time is more than 2 years. We say the failure times for the hard drive... Read more 20 Apr 2018 - 2 minute read

To precision or to variance?

Multivariate normal distributions are really nice. (Invertible) affine transformations, marginalization, and conditioning all preserve a multivariate normal distribution. In this post, I want to discuss marginalization and conditioning. In particular, I want to point out that computing the marginal distribution is easy when we parametrize wit... Read more 13 Apr 2018 - 1 minute read