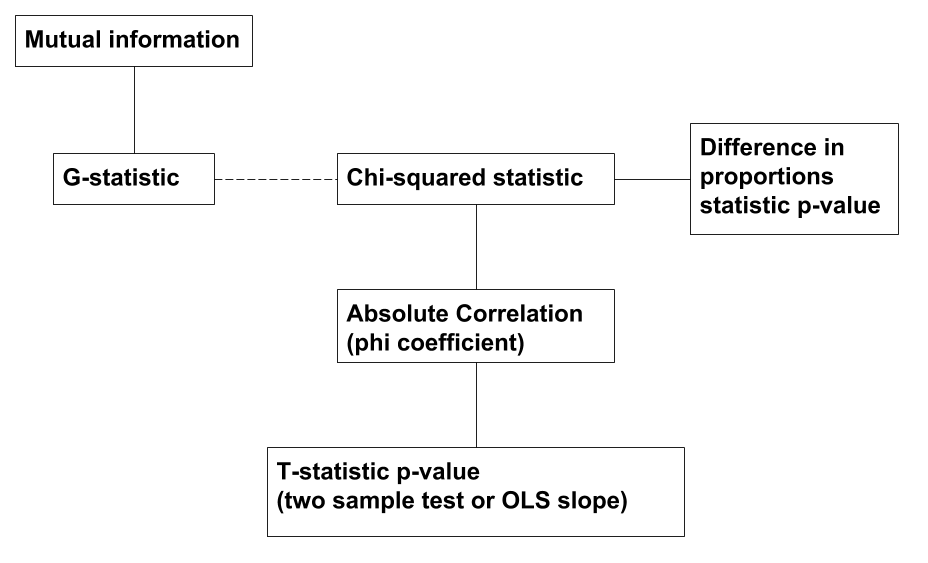
The relationship between correlation, mutual information, and p-values

Feature selection is often necessary before building a machine learning or statistical model, especially when there are many, many irrelevant features. To be more concrete, suppose we want to predict/explain some response \(Y\) using some features \(X_1, \ldots, X_k\). A natural first step is to find the features that are “most related” to the... Read more 03 Mar 2019 - 11 minute read

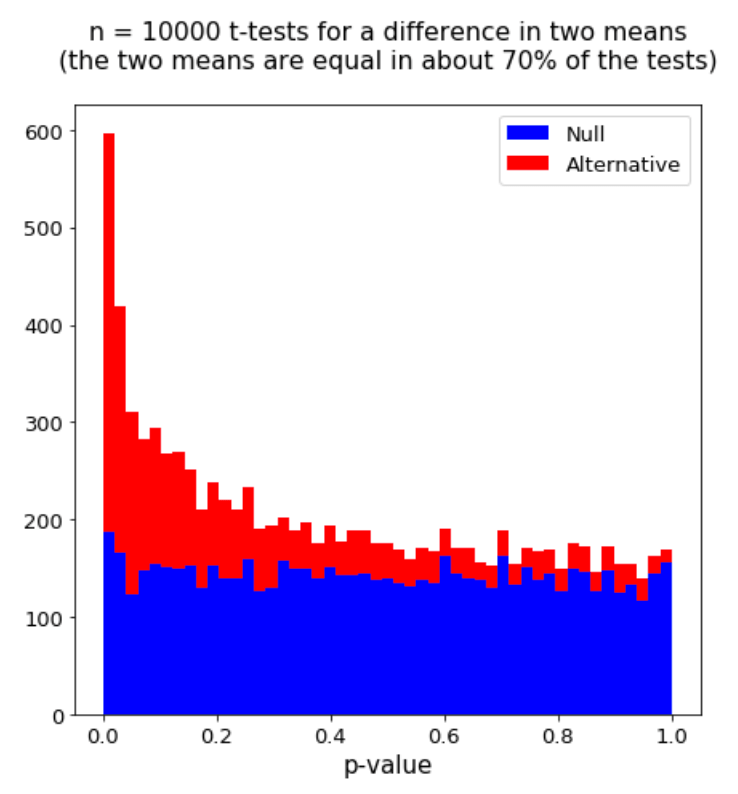
Controlling error when testing many hypotheses

In a hypothesis test, we compute some test statistic \(T\) that is designed to distinguish between a null and alternative hypothesis. We then compute the probability p(T) of observing a test statistic as large or more extreme as T under the null hypothesis, and reject the null hypothesis if the p-value p(T) is sufficiently small. (As an aside, ... Read more 18 Nov 2018 - 7 minute read

Calibration in logistic regression and other generalized linear models

In general, scores returned by machine learning models are not necessarily well-calibrated probabilities (see my post on ROC space and AUC). The probability estimates from a logistic regression model (without regularization) are partially calibrated, though. In fact, many generalized linear models, including linear regression, logistic regress... Read more 21 Aug 2018 - 13 minute read

Geometric interpretations of linear regression and ANOVA

In this post, I explore the connection of linear regression to geometry. In particular, I discuss the geometric meaning of fitted values, residuals, and degrees of freedom. Using geometry, I derive coefficient interpretations and discuss omitted variable bias. I finish by connecting ANOVA (both hypothesis testing and power analysis) to the un... Read more 05 Aug 2018 - 16 minute read

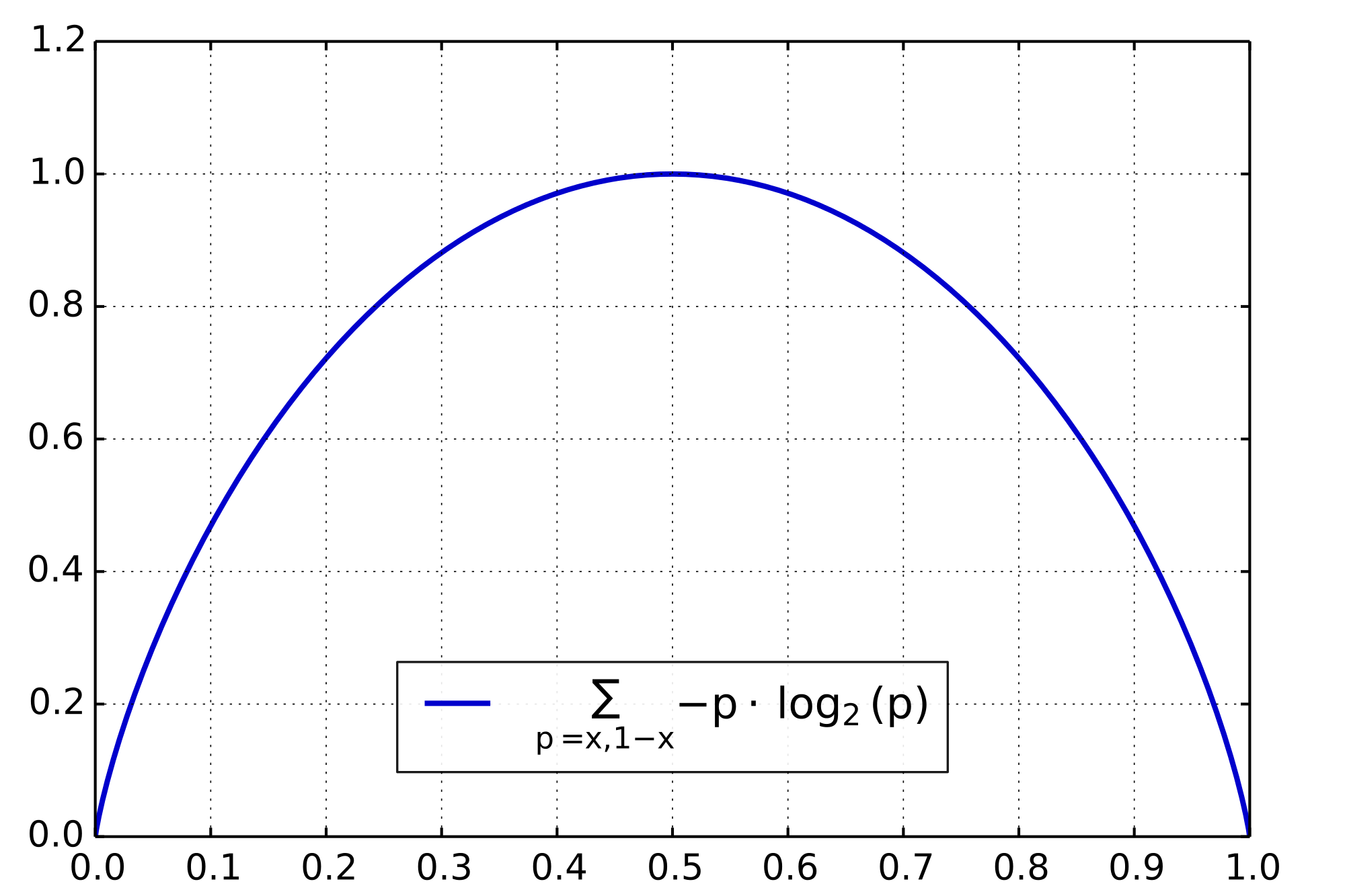
Inference based on entropy maximization

Entropy For a discrete random variable, the surprisal (or information content) of an outcome with probability \(p\) is \(-\log p\). Rare events have a lot surprisal. For a discrete random variable with \(n\) outcomes that occur with probabilities \(p_1, \ldots, p_n\), the entropy \(H\) is the average surprisal \[H(p_1,\ldots,p_n) = \sum_{i=1}... Read more 18 May 2018 - 3 minute read